Simon Barlovits | MathCityMap

In diesem Monat möchten wir einen Mathtrail aus Indonesien vorstellen: Hier hat unser MathCityMap-Educator Adi Nur Cahyono den “Telaga Tujuh Island Adventure Trail” angelegt. Zum neuen Piraten-Narrativ von MCM hat uns Adi Nur Cahyono einige Fragen beantwortet.

Wieso nutzt Du das Piraten-Narrativ?

Als ich erfuhr, dass die MathCityMap-App um eine Piratenerzählung ergänzt wird, habe ich sofort nach einer Route gesucht, welche besonders gut zu diesem Narrativ passt. Eine dieser Routen ist der Trail auf der Insel Telaga Tujuh. Durch die Piratengeschichte wirken Route und Aufgaben noch interessanter: Ein Abenteuer am Meer, bei welchem mathematische Probleme auf einer Insel gelöst werden müssen, welche nur per Schiff erreichbar ist – das klingt nach einer echten Piratenerzählung, oder?

Warum profitieren SchülerInnen von der Nutzung des Piraten-Narrativs?

SchülerInnen kennen viele Abenteuer, in welchen Piraten nach wertvollen Schätzen suchen. Und letztlich ist die Suche nach „mathematischen“ Schätzen die Idee des MathCityMap-Projekts. Die Kombination von MathCityMap mit einem Piratenabenteuer führt zu einem größeren Interesse der SchülerInnen, nämlich zum Erforschen des Trails aus Piratensicht bei gleichzeitigem Erlernen von Mathematik.

Was ist die Besonderheit des „Telaga Tujuh Island Adventure Trail“?

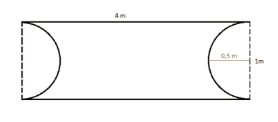
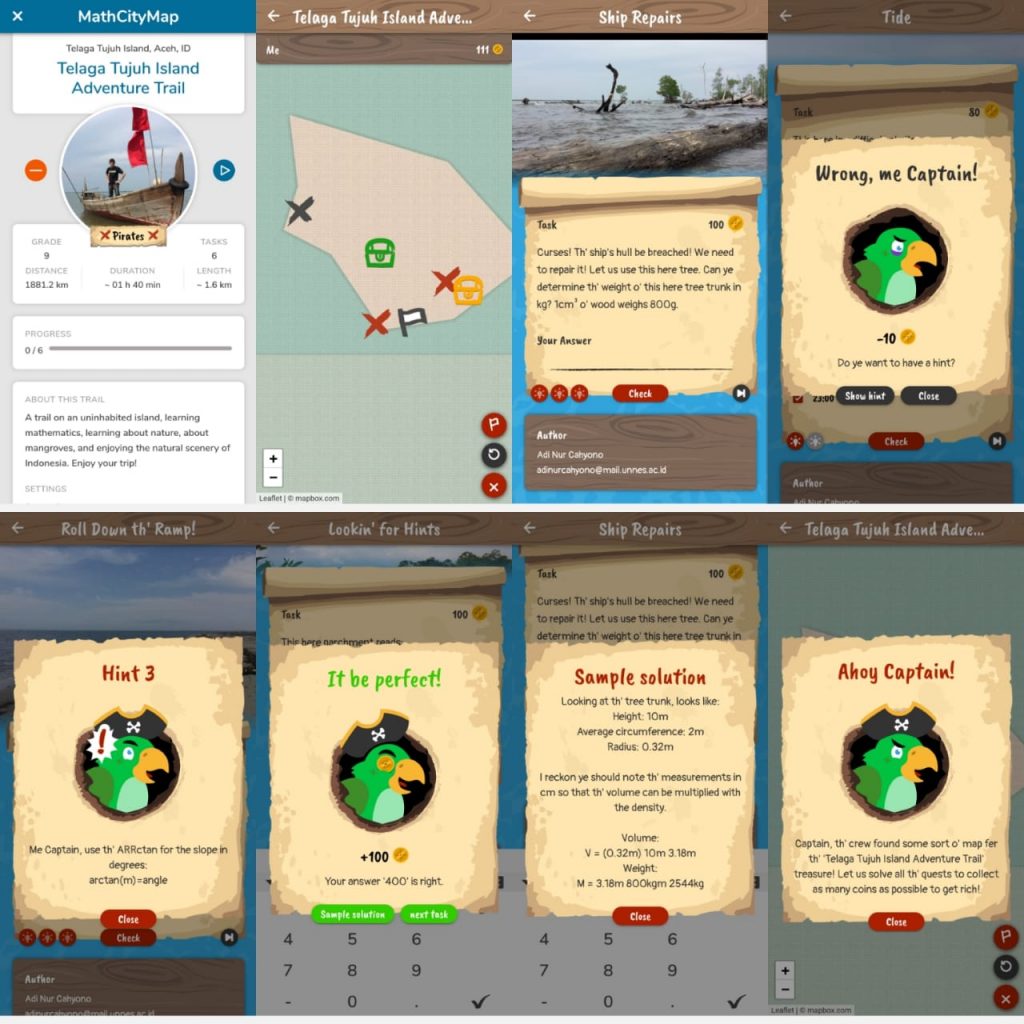
Der “Telaga Tujuh Adventure Trail” ist ein Mathtrail auf einer unbewohnten Insel in der indonesischen Provinz Aceh. Die Route habe ich erstellt, als ich nach passenden mathematischen Fragestellungen und Problemen zum neuen Piraten-Narrativ suchte. Ein Beispiel für eine solche, zur Piraten-Story passenden Aufgabe ist die Aufgabe zur Schiffsreparatur: „Beim Klabautermann! Das Schiff hat ein Leck. Wir müssen es schleunigst reparieren! Vielleicht können wir diesen Baumstamm hier verwenden. Käpt’n, die Crew muss wissen wie viel Kilogramm dieser Baumstamm wiegt. Ich habe von Landratten aufgeschnappt, dass 1cm³ des Holzes 600g wiegt.“

Durch die Bearbeitung des Trails können sich Nutzer auf eine mathematische Entdeckungsreise durch die wunderschöne Natur Indonesiens begeben. Discover MathCityMap, visit Indonesia!

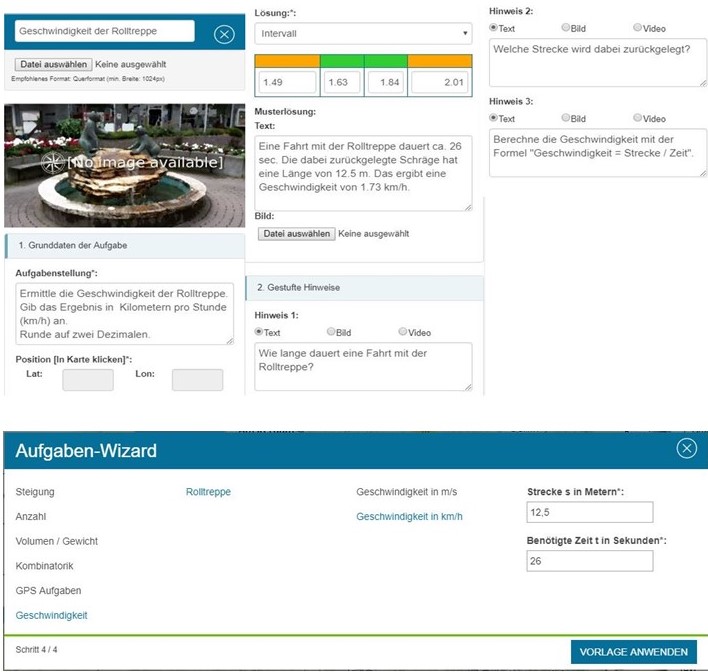
Good to know: Adi Nur Cahyono hat den “Telaga Tujuh Island Adventure Trail” erstellt, um das neue Piraten-Narrativ zu entdecken. Für seinen Trail nutzt er viele Wizard-Aufgaben, da diese in eine, zur Piraten-Story passende Geschichte eingebettet werden.

Matthias Ludwig stellt das MathCityMap-Projekt in Namibia vor!

An der J.G. Van der Wath Secondary School wurden in den vergangenen Tagen im Rahmen einer Lehrerfortbildung einige MathCityMap-Aufgaben erstellt und anschließend von den LehrerInnen getestet. So entstand beispielsweise die Aufgabe „The tire“ (dt.: der Reifen), bei welcher die Lernenden den Umfang eines im Boden versenkten Autoreifens ermitteln sollen.

Da sich die Teilnehmer der Fortbildung von MathCityMap begeistert zeigten, können wir uns auf viele weitere Aufgaben aus Okahandja freuen!

Bilder und weitere Informationen zu Matthias Ludwigs Reise nach Namibia finden Sie auf der MCM-Twitter-Seite.

Die heutige Aufgabe der Woche wurde in Druskininkai, Litauen, von unserer MoMaTrE-Projektpartnerin Sona Ceretkova erstellt. Die Aufgabenstellung „Flower Frame“ fragt, wie viel Prozent der Beetfläche aus einem Rechteck durch zwei halbkreisförmige Einschnitte „herausgeschnitten“ wurden. Zu ihrer Aufgabe hat uns Sona Ceretkova einige Fragen beantwortet.

Was ist der mathematische Gegenstand der Aufgabe?

Das Blumenbeet befindet sich im Kurort Druskininkai in Litauen, der als wahres Blumenparadies gilt. Es ist eine weit verbreitete Praxis, Blumenbeete durch Steinreihen zu rahmen. Ein solcher Steinrahmen wurde aufgrund seiner interessanten Form für unsere Aufgabe gewählt: Das Blumenbeet kann als Rechteck mit zwei ausgeschnittenen Halbkreisen modelliert werden.

Zu jenem Objekt sind eine Vielzahl mathematischer Fragestellungen denkbar:

Berechne die Größe der Rechtecksfläche ohne die kreisförmigen Einschnitte.
Berechne die Fläche der beiden Einschnitte.
Berechne die Differenz der Gesamtfläche des Rechtecks (ohne Einschnitte) und der beiden Einschnitte.
Berechne den Anteil der Einschnitte an der Rechtecksfläche.
Berechne den Anteil der Einschnitte an der Gesamtfläche des Blumenbeets.
Berechne, wie viel Prozent des Rechtecks durch die beiden Einschnitte fehlen.
Dies ist auch die Aufgabenstellung der hier präsentierten Aufgabe „Flower Frame“

Wie kann man das Problem lösen?

Die Rahmung des Blumenbeets hat „mathematikfreundliche“ Maße: Es ist vier Meter lang und einen Meter breit. Bei beiden Einschnitten handelt es sich um zwei identische Halbkreise, welche folglich einen ganzen Kreis bilden. Dies wird in einem Hinweis angegeben. Damit ist die gegebene geometrische Modelling der Situation relativ einfach (siehe Bild).

Ein weiterer Hinweis legt fest, dass die Fläche des Rechtecks (Fläche des Blumenbeets ohne Einschnitte) 100% beträgt. Damit beträgt die Größe der fehlenden Fläche ca. 20%. Die Lösung wird mittels multiple choise abgefragt, was wir in diesem Sachzusammenhang für das sinnvollste Lösungsformat erachten. Interessant kann es dabei sein, die Aufgabenbearbeiter vor der Vermessung einen Tipp abgeben zu lassen: Dass 1/5 der Rechtecksfläche durch die beiden halbkreisförmigen Einschnitte „herausgeschnitten“ wurden, ist ein überraschend großer Anteil!

Welches didaktische Ziel verfolgt die Aufgabe?

Mit dieser Aufgabenstellung wollen wir mehrere mathematikdidaktische Ziele verfolgen:

Präzises Messen.
Vorstellen, Zeichnen oder Beschreiben der mathematischen Situation durch ein Rechteck und zwei Halbkreise.
Berung zweier geometrischer Grundformen: Rechteck & Kreis
Korrekter Umgang mit Einheiten
Anwendung der Prozentrechnung
Interdisziplinäre Ansätze: Ökologie & Botanik

Unsere neue Aufgabe der Woche führt uns nach Irland: Auf dem Campus der Dublin City University (DCU) hat unser MoMatrE-Partner Christian Mercat die Aufgabe „Das Gewicht der DCU“ erstellt und uns einige Fragen über MathCityMap beantwortet.

Was ist der Gegenstand der Aufgabe?

Auf dem Campus ist ein riesiger Steinschriftzug zu finden. Ich habe mich gefragt, wie schwer dieser DCU-Schriftzug wohl ist. Daher habe ich die Figur eingehend untersucht und die Oberfläche sowie die Tiefe der Figuren vermessen.

Wie kann die Aufgabe gelöst werden?

Zunächst muss die die durchschnittliche Länge und Breite jedes Buchstaben ermittelt werden. So kann der Buchstabe „C“ als -Anteil eines Kreisrings zum Durchmesser 2 m mit einer Breite von 30 cm modelliert werden. Damit beträgt seine Oberfläche ca. 1,2 m². Die Modellierung der Buchstaben „D“ und „U“ erfolgt gleichermaßen. Insgesamt ergibt sich eine Oberfläche von 4,5 m². Bei einer gemessenen Tiefe von 50 cm führt dies zu einem Volumen von 2,25 m³. Die Dichte des verwendeten Steins beträgt ca. 2,4 t/m³. Somit beträgt das Gesamtgewicht der Skulptur ca. 5400 kg.

Da das Abschätzen der Skulpturenoberfläche knifflig ist, habe ich deren Größe numerisch mittels GeoGebra abgeschätzt (siehe Foto).

Abschätzung der Skulpturenoberfläche mittels GeoGebra.

Welches didaktische Ziel verfolgt die Aufgabe?

Natürlich geht es darum, dass die Schülerinnen und Schüler eine ungefähre Abschätzung vornehmen: Wiegt die Skulptur nur einige hundert Kilo, einige Tonnen oder gar zehn Tonnen? Ich habe ein relativ großes Lösungsintervall zwischen 3000 kg und 7500 kg zugelassen, falls die Lernenden die Aufgabe durch ein bloßes Vermessen mittels ihrer Arme lösen wollen. Dies halte ich für eine akzeptable Lösungsmethode. Jedoch zielt die Aufgabe eigentlich darauf ab, die Buchstaben möglichst genau geometrisch zu beschreiben. Für eine gute Lösung akzeptiere ich Angaben zwischen 5000 kg bis 6000 kg.

Warum nutzen Sie MathCityMap?

Ich liebe es, MathCityMap-Trails zu erstellen! Durch das Erstellen von MCM-Aufgaben lernt man die eigene Umgebung mit einem mathematikspezifischen Blick kennen. Die Suche nach mathematisch interessanten Objekten schult das „mathematische Auge”.

Unsere neue Aufgabe der Woche führt uns nach Lüneburg. Dort hat die Lehramtsstudentin Jennifer Oppermann die Aufgabe „Das grüne Ohr“ angelegt und uns einige Fragen beantwortet.

Worum geht es in der Aufgabe?

„Wie groß ist der Mensch, dem dieses Ohr gehört?“ lautet die Anwendungsaufgabe für „das grüne Ohr Lüneburgs“. Um diese Aufgabe zu lösen wird als Erstes das grüne Ohr in seiner Länge ausgemessen. Dasselbe wird mit dem Ohr eines beliebigen Menschen gemacht. Zusätzlich wird von dem Menschen die Körpergröße ermittelt. Anschließend wird die Länge des menschlichen Ohres durch die Länge des grünen Ohres dividiert. Der Quotient stellt das Verhältnis der beiden Längen dar. Zum Schluss wird die Körpergröße mit dem Verhältnis der beiden Ohren multipliziert. Das Produkt kann als ungefähre Größe des Menschen, dem das grüne Ohr gehört, interpretiert werden.

Da bei dieser Aufgabe auf das Verhältnis zwischen Ohr und Körpergröße geachtet werden soll, gibt es keine genaue Lösung. Das Verhältnis von Ohr und Körpergröße ist bei jedem Menschen unterschiedlich, weshalb die Lösung in einem Intervall liegt.

Welches didaktische Ziel verfolgt die Aufgabe?

Didaktisch dient die Aufgabe dazu, die inhaltsbezogenen Kompetenzen Raum und Form und Größen und Messen, sowie der prozessbezogenen Kompetenz mathematisches Modellieren zu vertiefen. Beim Modellieren geht es darum, einen Bezug zwischen der Mathematik und der Realität herzustellen. Dabei wird das Problem aus der Realität beginnend mit mathematischen Methoden gelöst und anschließend logisch überprüft. MathCityMap ist daher unterstützend, um Mathematik in der Umwelt und Kultur genauer wahrnehmen und anwenden zu können.

Wofür nutzen Sie MathCityMap?

Mit dem Ziel, zu Lernen die uns umgebene Welt aus einer mathematischen Perspektive zu sehen, erstellten wir einen eigenen mathematischen Rundgang durch die Hansestadt Lüneburg. MathCityMap nutzen wir daher als Hilfsmittel, damit Mathematikinteressierte aus der Region Lüneburg Aufgaben und Probleme aus der realen Welt mit einfachen mathematischen Mitteln bearbeiten können, um die eigenen mathematischen Kompetenzen zu steigern.

Das Erstellen eines Mathtrails ist zu aufwendig? Zu zeitraubend? Zu kompliziert? Wir beweisen das Gegenteil! Mit dem Aufgaben-Wizard können Aufgaben wie von Zauberhand erstellt werden. Wie das Tool funktioniert, stellen wir im Folgenden vor.

Notiz: Die folgende Beschreibung zum Aufgaben-Wizard erschien im August unter dem Titel „Mathe draußen: MathCityMap“ in der Fachzeitschrift mathematik lehren 2019 (215), S. 29-32.

Wizard-Aufgaben als mathematische „Standardsituationen“:

In jeder Stadt gibt es Treppen, Gebäude, Rampen und viele weitere immer wiederkehrende Objekte, an denen man aktiv Mathematik betreiben kann. An diesen Objekten haben wir „standardisierte“ Aufgaben wie beispielsweite die Bestimmung der Steigung einer Rampe oder die Berechnung des Gewichts eines quaderförmigen Steins im Webportal vorbereitet. Wir sprechen in diesem Zusammenhang von sogenannten „Generic Tasks“ oder auch „Blaupausenaufgaben“. Es handelt sich um didaktisch ausgearbeitete Vorlagen für vielfältige Aufgabenstellungen zu Themen der Kombinatorik, Algebra (Funktionen) und Geometrie.

Ein Beispiel – Geschwindigkeit der Rolltreppe:

Das Wizard-Prinzip wird am Beispiel der Aufgabe “Geschwindigkeit der Rolltreppe“ (Abb. 1) deutlich. Europäische Rolltreppen besitzen genormte Geschwindigkeiten (EN 115). Sie eignen sich daher insbesondere, um das Konzept der Geschwindigkeit im wahrsten Sinne zu erfahren und zu erleben. Man bewegt sich mit konstanter Geschwindigkeit entlang einer geraden Strecke. Der Aufgabenersteller benötigt für das Anlegen der Aufgabe lediglich die beiden Messwerte für benötigte Zeit und Länge der Treppe (Abb. 2).

Durch Eingabe in die Vorlage im Aufgaben-Wizard des Portals erstellt das System wie von Zauberhand eine MCM-Aufgabe, die nur noch durch ein Foto vom Objekt und die Aufgabenposition ergänzt werden muss.

Aufgabenstellung, Musterlösung, sowie eventuell notwendige Intervall-Berechnung und Hinweise werden automatisch vom Aufgaben-Wizard generiert, können aber, falls gewünscht, an die individuelle Situation oder die individuelle Lerngruppe und ihr Vorwissen angepasst werden.

Zusammenfassung & Schritt-für-Schritt-Anleitung:

Mit dem Wizard stellen wir allen Nutzern ein Tool zur Verfügung, wodurch „Generic Tasks“ bzw. „Blaupausenaufgaben schnell erstellt werden können. Die Erstellung von Wizard-Aufgaben erfolgt folgendermaßen:

Aufrufen des Reiters „Neue Aufgabe“ im MathCityMap-Portal.
„Wizard-Aufgabe“ auswählen – der Wizard öffnet sich.
Art der gewünschten Wizard-Aufgabe auswählen (z.B. Geschwindigkeit – Rolltreppe – Geschwindigkeit in m/s) und erhobene Messwerte
Aufgabenbild auswählen und ggf. Geoposition bestimmen. Fertig!

Wir wünschen allen Nutzern viel Spaß beim Ausprobieren!

Die Aufgabe der Woche ist zurück aus der Sommerpause! Heute möchten wir Euch eine Aufgabe vorstellen, die während einer MCM-Lehrerfortbildung am Georg-Büchner-Gymnasium in Bad Vilbel entstand.

Am Rande des Schulgeländes steht die abgebildete Skulptur einer Wasserflasche. Da drängt sich uns die Frage, wie viele Liter Wasser das Kunstwerk fassen würde, förmlich auf. Zur Modellierung der Aufgabe „Füllmenge der Flasche“ nehmen wir eine Wandstärke von 3 cm an.

Wie kann die Füllmenge berechnet werden?

Zur Modellierung bietet sich die Zerlegung des Kunstwerkes in einen Kegelstumpf (Flaschenhals) und einen Kreiszylinder (Flaschenbauch) an. Wir betrachten die Flasche also als zusammengesetzten Körper.

Worauf zielt die Aufgabe ab?

Die Herausforderung der Aufgabe besteht darin, eine sinnvolle Zerlegung für das Kunstwerk zu finden, welche das Objekt einerseits mathematisch sinnvoll beschreibt, andererseits aber auch mit einen bewältigbaren Rechenaufwand einhergeht. Daher steht unsere Aufgabe der Woche exemplarisch für viele reale Modellierungsprobleme: In realen Sachzusammenhängen muss – anders als im Schulbuch – oftmals ein Kompromiss zwischen mathematischer Exaktheit und anwendungsorientierter Effizienz gefunden werden. Gesucht wird also eine hinreichende Genauigkeit zur Beschreibung des realen Objekts!

Mathe ist langweilig, unverständlich und total kompliziert? Wir beweisen das Gegenteil!

Der Mathtrail „Land der Ideen WI-kurz“ zeigt, wo wir alltäglich in unserer Umwelt mit Mathematik konfrontiert sind. Durch genaues Beobachten, Zählen und Messen können die Aufgaben bereits von Schülerinnen und Schüler ab der 6. Klasse gelöst werden. So fragen wir beispielsweise, wie viele kreisrunde Fenster an der Fassade der Marktkirche zu entdecken sind, in welche Himmelsrichtung die Statue Wilhelm I. blickt oder wie oft sich eine Werbesäule pro Tag dreht.

Auch wer eine schwierige Herausforderung sucht, wird nicht enttäuscht: In unmittelbarer Nähe haben wir den Trail „Land der Ideen WI-lang“ angelegt, welcher für Schülerinnen und Schüler ab der 9. Klasse geeignet ist.

Wir wünschen viel Spaß beim Ausprobieren der Trails, welche wir zur Ausstellung des „Land der Ideen“-Wettbewerbs in Wiesbaden erstellt haben.

Mehr zum Thema:
– MathCityMap gewinnt „Land der Ideen“-Auszeichnung
– Das MathCityMap-Team bei der „Land der Ideen“-Preisverleihung
– Das „Land der Ideen“-Team zu Gast bei MathCityMap
– Ausstellung zum „Land der Ideen“ in Wiesbaden

Das MathCityMap-Projekt wurde 2019 vom „Land der Ideen“-Wettbewerb ausgezeichnet! Die zehn Preisträger werden aktuell in einer Ausstellung in einer Filiale der Deutschen Bank (Wilhelmstraße 20-22) in Wiesbaden vorgestellt.

Als ideale Ergänzung zur Ausstellung gibt es nun auch zwei MathCityMap-Mathtrails zwischen dem Ausstellungsort und der Wiesbadener Marktkirche: Der Trail „Land der Ideen WI-kurz“ ist bereits für SchülerInnen der 6. Klasse zu empfehlen. Hier geht es darum, die Umwelt durch genaues Beobachten, Zählen und Messen zu erfahren. Den Trail „Land der Ideen WI-lang“ empfehlen wir ab der 9. Klasse.

Wir wünschen viel Spaß beim Ausprobieren der Trails!

Autor: Simon Barlovits

Trail des Monats: Ein Piratenabenteuer auf Telaga Tujuh

MathCityMap zu Gast in Namibia

Aufgabe der Woche: Das Blumenbeet

Aufgabe der Woche: Das Gewicht der DCU

Aufgabe der Woche: Das grüne Ohr

Der Wizard: Aufgaben wie von Zauberhand!

Aufgabe der Woche: Füllmenge der Flasche

Der Trail des Monats: „Land der Ideen WI-kurz“

Ausstellung zum „Land der Ideen“ in Wiesbaden