Aufgabe der Woche | MathCityMap

Aufgabe der Woche: Das Blumenbeet

Die heutige Aufgabe der Woche wurde in Druskininkai, Litauen, von unserer MoMaTrE-Projektpartnerin Sona Ceretkova erstellt. Die Aufgabenstellung „Flower Frame“ fragt, wie viel Prozent der Beetfläche aus einem Rechteck durch zwei halbkreisförmige Einschnitte „herausgeschnitten“ wurden. Zu ihrer Aufgabe hat uns Sona Ceretkova einige Fragen beantwortet. Was ist der mathematische Gegenstand der Aufgabe? Das Blumenbeet befindet sich […]

Die heutige Aufgabe der Woche wurde in Druskininkai, Litauen, von unserer MoMaTrE-Projektpartnerin Sona Ceretkova erstellt. Die Aufgabenstellung „Flower Frame“ fragt, wie viel Prozent der Beetfläche aus einem Rechteck durch zwei halbkreisförmige Einschnitte „herausgeschnitten“ wurden. Zu ihrer Aufgabe hat uns Sona Ceretkova einige Fragen beantwortet.

Was ist der mathematische Gegenstand der Aufgabe?

Das Blumenbeet befindet sich im Kurort Druskininkai in Litauen, der als wahres Blumenparadies gilt. Es ist eine weit verbreitete Praxis, Blumenbeete durch Steinreihen zu rahmen. Ein solcher Steinrahmen wurde aufgrund seiner interessanten Form für unsere Aufgabe gewählt: Das Blumenbeet kann als Rechteck mit zwei ausgeschnittenen Halbkreisen modelliert werden.

Zu jenem Objekt sind eine Vielzahl mathematischer Fragestellungen denkbar:

Berechne die Größe der Rechtecksfläche ohne die kreisförmigen Einschnitte.
Berechne die Fläche der beiden Einschnitte.
Berechne die Differenz der Gesamtfläche des Rechtecks (ohne Einschnitte) und der beiden Einschnitte.
Berechne den Anteil der Einschnitte an der Rechtecksfläche.
Berechne den Anteil der Einschnitte an der Gesamtfläche des Blumenbeets.
Berechne, wie viel Prozent des Rechtecks durch die beiden Einschnitte fehlen.
Dies ist auch die Aufgabenstellung der hier präsentierten Aufgabe „Flower Frame“

Wie kann man das Problem lösen?

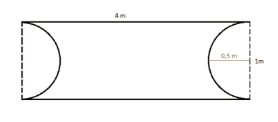
Die Rahmung des Blumenbeets hat „mathematikfreundliche“ Maße: Es ist vier Meter lang und einen Meter breit. Bei beiden Einschnitten handelt es sich um zwei identische Halbkreise, welche folglich einen ganzen Kreis bilden. Dies wird in einem Hinweis angegeben. Damit ist die gegebene geometrische Modelling der Situation relativ einfach (siehe Bild).

Ein weiterer Hinweis legt fest, dass die Fläche des Rechtecks (Fläche des Blumenbeets ohne Einschnitte) 100% beträgt. Damit beträgt die Größe der fehlenden Fläche ca. 20%. Die Lösung wird mittels multiple choise abgefragt, was wir in diesem Sachzusammenhang für das sinnvollste Lösungsformat erachten. Interessant kann es dabei sein, die Aufgabenbearbeiter vor der Vermessung einen Tipp abgeben zu lassen: Dass 1/5 der Rechtecksfläche durch die beiden halbkreisförmigen Einschnitte „herausgeschnitten“ wurden, ist ein überraschend großer Anteil!

Welches didaktische Ziel verfolgt die Aufgabe?

Mit dieser Aufgabenstellung wollen wir mehrere mathematikdidaktische Ziele verfolgen:

Präzises Messen.
Vorstellen, Zeichnen oder Beschreiben der mathematischen Situation durch ein Rechteck und zwei Halbkreise.
Berung zweier geometrischer Grundformen: Rechteck & Kreis
Korrekter Umgang mit Einheiten
Anwendung der Prozentrechnung
Interdisziplinäre Ansätze: Ökologie & Botanik

Aufgabe der Woche: Das Gewicht der DCU

Unsere neue Aufgabe der Woche führt uns nach Irland: Auf dem Campus der Dublin City University (DCU) hat unser MoMatrE-Partner Christian Mercat die Aufgabe „Das Gewicht der DCU“ erstellt und uns einige Fragen über MathCityMap beantwortet. Was ist der Gegenstand der Aufgabe? Auf dem Campus ist ein riesiger Steinschriftzug zu finden. Ich habe mich gefragt, […]

Unsere neue Aufgabe der Woche führt uns nach Irland: Auf dem Campus der Dublin City University (DCU) hat unser MoMatrE-Partner Christian Mercat die Aufgabe „Das Gewicht der DCU“ erstellt und uns einige Fragen über MathCityMap beantwortet.

Was ist der Gegenstand der Aufgabe?

Auf dem Campus ist ein riesiger Steinschriftzug zu finden. Ich habe mich gefragt, wie schwer dieser DCU-Schriftzug wohl ist. Daher habe ich die Figur eingehend untersucht und die Oberfläche sowie die Tiefe der Figuren vermessen.

Wie kann die Aufgabe gelöst werden?

Zunächst muss die die durchschnittliche Länge und Breite jedes Buchstaben ermittelt werden. So kann der Buchstabe „C“ als -Anteil eines Kreisrings zum Durchmesser 2 m mit einer Breite von 30 cm modelliert werden. Damit beträgt seine Oberfläche ca. 1,2 m². Die Modellierung der Buchstaben „D“ und „U“ erfolgt gleichermaßen. Insgesamt ergibt sich eine Oberfläche von 4,5 m². Bei einer gemessenen Tiefe von 50 cm führt dies zu einem Volumen von 2,25 m³. Die Dichte des verwendeten Steins beträgt ca. 2,4 t/m³. Somit beträgt das Gesamtgewicht der Skulptur ca. 5400 kg.

Da das Abschätzen der Skulpturenoberfläche knifflig ist, habe ich deren Größe numerisch mittels GeoGebra abgeschätzt (siehe Foto).

Abschätzung der Skulpturenoberfläche mittels GeoGebra.

Welches didaktische Ziel verfolgt die Aufgabe?

Natürlich geht es darum, dass die Schülerinnen und Schüler eine ungefähre Abschätzung vornehmen: Wiegt die Skulptur nur einige hundert Kilo, einige Tonnen oder gar zehn Tonnen? Ich habe ein relativ großes Lösungsintervall zwischen 3000 kg und 7500 kg zugelassen, falls die Lernenden die Aufgabe durch ein bloßes Vermessen mittels ihrer Arme lösen wollen. Dies halte ich für eine akzeptable Lösungsmethode. Jedoch zielt die Aufgabe eigentlich darauf ab, die Buchstaben möglichst genau geometrisch zu beschreiben. Für eine gute Lösung akzeptiere ich Angaben zwischen 5000 kg bis 6000 kg.

Warum nutzen Sie MathCityMap?

Ich liebe es, MathCityMap-Trails zu erstellen! Durch das Erstellen von MCM-Aufgaben lernt man die eigene Umgebung mit einem mathematikspezifischen Blick kennen. Die Suche nach mathematisch interessanten Objekten schult das „mathematische Auge”.

Aufgabe der Woche: Das grüne Ohr

Unsere neue Aufgabe der Woche führt uns nach Lüneburg. Dort hat die Lehramtsstudentin Jennifer Oppermann die Aufgabe „Das grüne Ohr“ angelegt und uns einige Fragen beantwortet. Worum geht es in der Aufgabe? „Wie groß ist der Mensch, dem dieses Ohr gehört?“ lautet die Anwendungsaufgabe für „das grüne Ohr Lüneburgs“. Um diese Aufgabe zu lösen […]

Unsere neue Aufgabe der Woche führt uns nach Lüneburg. Dort hat die Lehramtsstudentin Jennifer Oppermann die Aufgabe „Das grüne Ohr“ angelegt und uns einige Fragen beantwortet.

Worum geht es in der Aufgabe?

„Wie groß ist der Mensch, dem dieses Ohr gehört?“ lautet die Anwendungsaufgabe für „das grüne Ohr Lüneburgs“. Um diese Aufgabe zu lösen wird als Erstes das grüne Ohr in seiner Länge ausgemessen. Dasselbe wird mit dem Ohr eines beliebigen Menschen gemacht. Zusätzlich wird von dem Menschen die Körpergröße ermittelt. Anschließend wird die Länge des menschlichen Ohres durch die Länge des grünen Ohres dividiert. Der Quotient stellt das Verhältnis der beiden Längen dar. Zum Schluss wird die Körpergröße mit dem Verhältnis der beiden Ohren multipliziert. Das Produkt kann als ungefähre Größe des Menschen, dem das grüne Ohr gehört, interpretiert werden.

Da bei dieser Aufgabe auf das Verhältnis zwischen Ohr und Körpergröße geachtet werden soll, gibt es keine genaue Lösung. Das Verhältnis von Ohr und Körpergröße ist bei jedem Menschen unterschiedlich, weshalb die Lösung in einem Intervall liegt.

Welches didaktische Ziel verfolgt die Aufgabe?

Didaktisch dient die Aufgabe dazu, die inhaltsbezogenen Kompetenzen Raum und Form und Größen und Messen, sowie der prozessbezogenen Kompetenz mathematisches Modellieren zu vertiefen. Beim Modellieren geht es darum, einen Bezug zwischen der Mathematik und der Realität herzustellen. Dabei wird das Problem aus der Realität beginnend mit mathematischen Methoden gelöst und anschließend logisch überprüft. MathCityMap ist daher unterstützend, um Mathematik in der Umwelt und Kultur genauer wahrnehmen und anwenden zu können.

Wofür nutzen Sie MathCityMap?

Mit dem Ziel, zu Lernen die uns umgebene Welt aus einer mathematischen Perspektive zu sehen, erstellten wir einen eigenen mathematischen Rundgang durch die Hansestadt Lüneburg. MathCityMap nutzen wir daher als Hilfsmittel, damit Mathematikinteressierte aus der Region Lüneburg Aufgaben und Probleme aus der realen Welt mit einfachen mathematischen Mitteln bearbeiten können, um die eigenen mathematischen Kompetenzen zu steigern.

Aufgabe der Woche: Füllmenge der Flasche

Die Aufgabe der Woche ist zurück aus der Sommerpause! Heute möchten wir Euch eine Aufgabe vorstellen, die während einer MCM-Lehrerfortbildung am Georg-Büchner-Gymnasium in Bad Vilbel entstand. Am Rande des Schulgeländes steht die abgebildete Skulptur einer Wasserflasche. Da drängt sich uns die Frage, wie viele Liter Wasser das Kunstwerk fassen würde, förmlich auf. Zur Modellierung der […]

Die Aufgabe der Woche ist zurück aus der Sommerpause! Heute möchten wir Euch eine Aufgabe vorstellen, die während einer MCM-Lehrerfortbildung am Georg-Büchner-Gymnasium in Bad Vilbel entstand.

Am Rande des Schulgeländes steht die abgebildete Skulptur einer Wasserflasche. Da drängt sich uns die Frage, wie viele Liter Wasser das Kunstwerk fassen würde, förmlich auf. Zur Modellierung der Aufgabe „Füllmenge der Flasche“ nehmen wir eine Wandstärke von 3 cm an.

Wie kann die Füllmenge berechnet werden?

Zur Modellierung bietet sich die Zerlegung des Kunstwerkes in einen Kegelstumpf (Flaschenhals) und einen Kreiszylinder (Flaschenbauch) an. Wir betrachten die Flasche also als zusammengesetzten Körper.

Worauf zielt die Aufgabe ab?

Die Herausforderung der Aufgabe besteht darin, eine sinnvolle Zerlegung für das Kunstwerk zu finden, welche das Objekt einerseits mathematisch sinnvoll beschreibt, andererseits aber auch mit einen bewältigbaren Rechenaufwand einhergeht. Daher steht unsere Aufgabe der Woche exemplarisch für viele reale Modellierungsprobleme: In realen Sachzusammenhängen muss – anders als im Schulbuch – oftmals ein Kompromiss zwischen mathematischer Exaktheit und anwendungsorientierter Effizienz gefunden werden. Gesucht wird also eine hinreichende Genauigkeit zur Beschreibung des realen Objekts!

Aufgabe der Woche: Das Sechseck

Diesmal ist die Aufgabe der Woche in Grahamstown, Südafrika. Berechnen Sie die Fläche der sechseckigen Tischfläche. Geben Sie das Ergebnis in Einheiten von m² an. Die Aufgabe kann auf verschiedene Arten gelöst werden. Einmal kann man die Fläche in sechs gleichschenklige Dreiecke aufteilen. Es ist auch möglich die Fläche in ein Rechteck und zwei Dreiecke […]

Diesmal ist die Aufgabe der Woche in Grahamstown, Südafrika.

Berechnen Sie die Fläche der sechseckigen Tischfläche. Geben Sie das Ergebnis in Einheiten von m² an.

Die Aufgabe kann auf verschiedene Arten gelöst werden. Einmal kann man die Fläche in sechs gleichschenklige Dreiecke aufteilen. Es ist auch möglich die Fläche in ein Rechteck und zwei Dreiecke zu unterteilen.

Aufgabe der Woche: Das Volumen von Mendeleïv

Diesmal ist die Aufgabe in Bratislava, Slowakei. Dmitri Ivanovitch Mendeleïev (Дмитрий Иванович Менделеев) hat das Periodensystem der Elemente aufgestellt, die als Strahlen um die Skulptur seines Porträts angeordnet sind. Berechnen Sie das Volumen dieser Skulptur in Kubikmetern. Die Skulptur hat die Form einer Halbkugel. Daher kann das Volumen mithilfe des Durchmesser berechnet werden.

Diesmal ist die Aufgabe in Bratislava, Slowakei.

Dmitri Ivanovitch Mendeleïev (Дмитрий Иванович Менделеев) hat das Periodensystem der Elemente aufgestellt, die als Strahlen um die Skulptur seines Porträts angeordnet sind.

Berechnen Sie das Volumen dieser Skulptur in Kubikmetern.

Die Skulptur hat die Form einer Halbkugel. Daher kann das Volumen mithilfe des Durchmesser berechnet werden.

Aufgabe der Woche: Das Krokodil am Goldfischteich

Heute spricht MCM mit Jörg Kleinsteuber (MCM Educator) über die Aufgabe der Woche in Apolda, Deutschland. Wenn das Holzkrokodil zum Leben erwachen und fressen würde, hätten die Goldfische „schlechte Karten“. Entscheide welche Menge an Nahrung ein ausgewachsenes 6 Meter-Exemplar im Vergleich zu einem Krokodil in der Größe des Holzkrokodils benötigen würde. Worum geht es bei […]

Heute spricht MCM mit Jörg Kleinsteuber (MCM Educator) über die Aufgabe der Woche in Apolda, Deutschland.

Wenn das Holzkrokodil zum Leben erwachen und fressen würde, hätten die Goldfische „schlechte Karten“. Entscheide welche Menge an Nahrung ein ausgewachsenes 6 Meter-Exemplar im Vergleich zu einem Krokodil in der Größe des Holzkrokodils benötigen würde.

Worum geht es bei der Aufgabe?

Das sehr schön geschnitzte Holzmodell ist eine Verkleinerung (zentrische Streckung) eines Krokodils. Da die Länge eines ausgewachsenen Krokodils ein Vielfaches vom Modell ist, lies sich diese ungewöhnliche Aufgabe daraus erstellen. Schon im Buch „Gullivers Reisen“ von Jonathan Swift bekam der 12x größere Gulliver die Kleidung (Fläche) von 144 Liliputanern und seine Essensportion hätte für 1728 von den Winzlingen gereicht. Diese mathematische Wirkung des Streckungsfaktors auf die Fläche und das Volumen ist immer wieder verblüffend. Ich habe als Antwortformat Multiple Choice gewählt, weil es mir bei dieser Aufgabe nicht um das exakte Messen, sondern um Verständnis und Anwendung von Wissen ging.

Zu welchem Zweck wurde die Aufgabe erstellt?

Die Aufgabe hatte ich für einen Workshop mit Lehrerinnen und Lehrern zur SINUS-Landestagung https://www.schulportal-thueringen.de/sinus_thueringen in Apolda (im Hotel Am Schloss https://www.hotel-apolda.de/ ) vorbereitet.

Als wir dann zur Tagung anreisten, bekam ich einen Schreck – das Krokodil war weg … und damit die Aufgabe nicht mehr lösbar. L

Der Tagungsleiter sprach deswegen mit dem Hotelpersonal und der Hausmeister holte daraufhin das Krokodil aus dem Winterschlaf aus dem Keller (super Service; Danke!)

So konnten die Teilnehmer doch noch diese ungewöhnliche Aufgabe lösen; es war eine harte „Nuss“, die aber Spaß gemacht hat. J

Ich habe danach sogar überlegt, ob ich das Foto austausche, damit man anhand der Lage des Krokodils seine Größe ermitteln kann, auch wenn es im Winter im Keller schläft.

Was gefällt Ihnen an MathCityMap?

Mich fasziniert an MCM die Kombination von klassischer Mathematik mit digitaler Unterstützung. Die Mathematik muss nicht komplizierte Rechnungen und aufwändige Anwendungen bedeuten. Kleine Aufgaben mit praktischem Bezug, bei denen die SuS selbst AKTIV werden müssen, indem sie messen, modellieren, schätzen, in Kleingruppen diskutieren bieten reichlich Potenzial für Schülertätigkeiten.

Die Möglichkeit das Smartphone als Unterstützung zu verwenden ist für die SuS selbstverständlich und zugleich motivationsfördernd. Gleichzeitig verringert sich dadurch mein Aufwand bei der Betreuung, denn die APP liefert Feedback in Form von Hinweisen, Musterlösungen und bietet auch Gamification (Punkte). Eine tolle Mischung!

Das neue „digitalen Klassenzimmer“ ermöglicht mir, mit den SuS während der Bearbeitung von Aufgaben zu chatten (Fragen zu beantworten) und Ihre Laufwege während der Teilnahme nachvollziehen.

In der Nachbereitung im Unterricht kommen sehr anregende Diskussionen zustande.

Vielen Dank für das Interview und dein Engagement für MCM!

Aufgabe der Woche: Pilz am Kaiserdomgymnasium

Diesmal stellen wir eine Aufgabe aus Speyer vor. Bei dem Objekt handelt es sich um beliebte Skulptur des Künstlers Wolf Spitzer. „Sigillum“, Bronze 1994, Siegelstempel – Planetengetriebe, das sich um die eigene Achse dreht und die nahe Museumsmauer tangiert. Das Sigillum stellt die Bewahrung von Geschichte und Kultur dar. Die Form der Figur wird von […]

Diesmal stellen wir eine Aufgabe aus Speyer vor. Bei dem Objekt handelt es sich um beliebte Skulptur des Künstlers Wolf Spitzer.

„Sigillum“, Bronze 1994, Siegelstempel – Planetengetriebe, das sich um die eigene Achse dreht und die nahe Museumsmauer tangiert. Das Sigillum stellt die Bewahrung von Geschichte und Kultur dar.

Die Form der Figur wird von den Anwohnern oft als Pilz interpretiert, daher der Name der Aufgabe. Geometrisch betrachtet handelt es sich um zwei, zusammengesetzte Zylinder.

Berechne das Volumen und gib das Ergebnis in Litern an! Ein Liter entspricht 1 dm³.

Bei dem großen Zylinder ist es schwierig den Umfang zu messen. Dagegen ist es einfach den Durchmesser zu erheben. Bei dem kleinen Zylinder ist es dagegen nicht schwer den Umfang zu messen. Es ist daher sehr wahrscheinlich, dass man beim Bearbeiten der Aufgabe verschiedene Wege geht, um das Volumen der beiden Teilkörper zu berechnen.

Erhebt man die Messwerte in Dezimeter erhält man als Summe der beiden Volumina direkt das Ergebnis.

Aufgabe der Woche: Ernst-Abbe Denkmal

Die Aufgabe der Woche dreht sich diesmal um das Ernst-Abbe Denkmal in Jena, Deutschland. Wie oft passt das Volumen der Kugel in den Pyramidenstumpf? Um die Aufgabe zu lösen müssen die Kugel und der Pyramidenstumpf vermessen werden, um das Volumen berechnen zu können. Anschließend dividiert man beide Größen. Das interessante an dieser Aufgabe ist, dass […]

Die Aufgabe der Woche dreht sich diesmal um das Ernst-Abbe Denkmal in Jena, Deutschland.

Wie oft passt das Volumen der Kugel in den Pyramidenstumpf?

Um die Aufgabe zu lösen müssen die Kugel und der Pyramidenstumpf vermessen werden, um das Volumen berechnen zu können. Anschließend dividiert man beide Größen. Das interessante an dieser Aufgabe ist, dass eine besondere Zahl im Lösungsintervall enthalten ist.

Aufgabe der Woche: Einfahrt verboten

Diesmal befindet sich die Aufgabe der Woche auf dem Gelände der VW Autostadt in Wolfsburg. Auf dem Verkehrsübungsplatz ist alles etwas kleiner als es in Wirklichkeit ist. Ein „Einfahrt verboten“ Schild hat normalerweise einen Durchmesser von 42cm. Wie viel größer ist ein normales Schild als das hier verwendete? Um die Aufgabe zu lösen, muss zunächst […]

Diesmal befindet sich die Aufgabe der Woche auf dem Gelände der VW Autostadt in Wolfsburg.

Auf dem Verkehrsübungsplatz ist alles etwas kleiner als es in Wirklichkeit ist. Ein „Einfahrt verboten“ Schild hat normalerweise einen Durchmesser von 42cm. Wie viel größer ist ein normales Schild als das hier verwendete?

Um die Aufgabe zu lösen, muss zunächst der Durchmesser des Schildes gemessen werden. Anschließend müssen die Flächeninhalte des kleinen und des normalen Schildes berechnet und in ein Verhältnis gesetzt werden. Als Ergebnis erhält man den Skalierungsfaktor der Fläche.