task of the week | MathCityMap

Task of the Week: The Wheel of Brisbane

We are welcoming the Australian tasks created by Adi Nur Cahyono, lecturer of mathematics education in Indonesia, in Brisbane. In an interview, he will give us an insight into his task idea “The Wheel of Brisbane”. Task: The Wheel of Brisbane (Task Number: 4638) If the speed of the wheel is 16 km / h, […]

We are welcoming the Australian tasks created by Adi Nur Cahyono, lecturer of mathematics education in Indonesia, in Brisbane. In an interview, he will give us an insight into his task idea “The Wheel of Brisbane”.

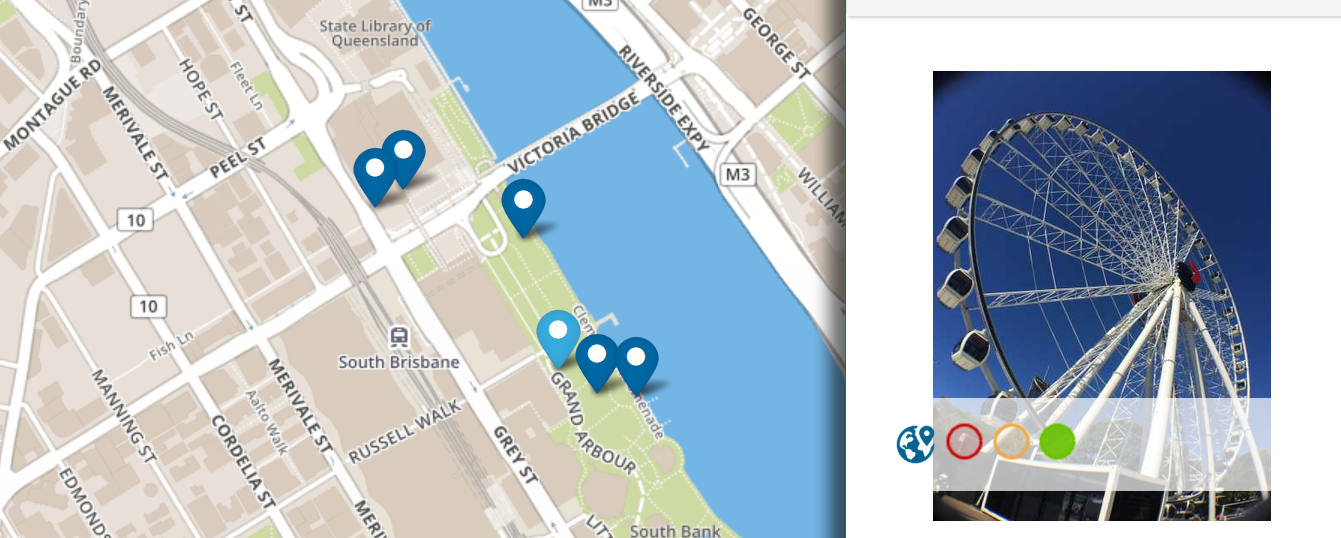
Task: The Wheel of Brisbane (Task Number: 4638)

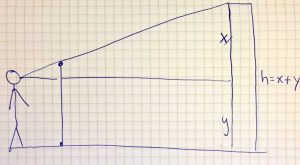
If the speed of the wheel is 16 km / h, how many seconds a person in the capsule can reach the top of the wheel since the capsule departs from the lowest part of the wheel?

What is the task about?

This task is about the application of congruence concept to measure the height of the Ferris wheel located at the south Bank of Brisbane. This is then combined with the application of the concept of time and velocity. This task intends to show that there are several things in the object and how it works that are related to mathematical concepts. Mathematical concepts can be used to determine when a person can reach a certain position on the wheel. Of course, this is not so important to know, we just want to enjoy the wheel. But it can be analogous to know the working of other objects that are similar, for example: windmills, car wheels, etc. But in general, choosing a tourist object to learn mathematics is a good and interesting thing.

What are your further plans within the MathCityMap-project?

My plan, and also my responsibility, is to expand the implementation of MCM in Indonesia and several countries in Asia and Australia through cooperation with universities. In Indonesia, implementation needs to be extended to other islands outside Java. Not only expansion of its implementation, I plan to develop it continuously, because technology develops and changes continuously, and implementation in different places also requires new innovations. Still connecting and working with MCM Team and being part of the MCM Team is an award for me.

Task of the Week: Roof Dome of the Diana Temple

Our current Task of the Week was created during the MNU meeting in Munich. The city offers great architectural possibilities to use MathCityMap, for example the Diana Temple in the Hofgarten. Task: Roof Dome of the Diana Temple (Task Number: 4513) Determine the size of the roof dome of the Diana Temple. Give the result […]

Our current Task of the Week was created during the MNU meeting in Munich. The city offers great architectural possibilities to use MathCityMap, for example the Diana Temple in the Hofgarten.

Task: Roof Dome of the Diana Temple (Task Number: 4513)

Determine the size of the roof dome of the Diana Temple. Give the result in m².

You can model the roof dome as a semi sphere and approximate the asked size by means of its surface. First, the radius of the semi sphere is determined using the diameter at the bottom. Using the formula for the surface of a sphere or divided by two of a semi sphere results the surface. Nevertheless, to approximate the result exactly, the stone triangles should be substracted. In total, there are four trinagles wholes surface area should be estimate due to the height and subtracted.

Task of the Week: Water in the Fountain

Fountains and their volume are ideal for modeling different geometric bodies. While many of the fountains have a rectangular or circular shape and can thus be approximated as cuboid or cylinder, in the current “Task of the Week” we present an octagonal fountain whose volume can be described by a prism with an octagonal area. […]

Fountains and their volume are ideal for modeling different geometric bodies. While many of the fountains have a rectangular or circular shape and can thus be approximated as cuboid or cylinder, in the current “Task of the Week” we present an octagonal fountain whose volume can be described by a prism with an octagonal area.

Task: Water in the Fountain (Task Number: 4295)

What is the approximate volume of water in this fountain? Assume that the average depth of the water is about 30 cm. Give the result in liters.

Even if the formula for an octagon is not known, the task can be solved by dividing the area or completing the area. For example, one can determine the area of the square enclosing the octagon. Then, for each corner which is calculated too much in the square, the area of a triangle must be substracted. The height is then used to calculate the volume.

Task of the Week: Cobblestones

As part of the ICM conference in Rio de Janeiro, Iwan Gurjanow created the first tasks in South America. In the resulting trail, our current Task of the Week is included. Task: Cobblestones (Task number: 4505) How many cobblestones are approximately in the highlighted area? While we have often used the task on circular or […]

As part of the ICM conference in Rio de Janeiro, Iwan Gurjanow created the first tasks in South America. In the resulting trail, our current Task of the Week is included.

Task: Cobblestones (Task number: 4505)

How many cobblestones are approximately in the highlighted area?

While we have often used the task on circular or rectangular surfaces, the parallelogram is focused here. It makes sense to determine the surface area and to count the number of stones in a certain range, e.g. in a square of size 60x60cm marked with the folding ruler. This number is then multiplied up to the total area, the area which quickly results from side length and height of the parallelogram.

A time-saving alternative to tedious counting, because the solution is highly above 1000.

Task of the Week: Direction

With our GPS tasks, such as the walking of a north-south line, we have already presented a first way how to connect the directions with MathCityMap. But many statues also offer the opportunity to implement the theme, for example, the monument of Maximilian of Bavaria in Munich. Task: Maximilian’s Pointer (Task number: 4483) In which […]

With our GPS tasks, such as the walking of a north-south line, we have already presented a first way how to connect the directions with MathCityMap. But many statues also offer the opportunity to implement the theme, for example, the monument of Maximilian of Bavaria in Munich.

Task: Maximilian’s Pointer (Task number: 4483)

In which direction does the right finger of Maximilian point? Give the result in degrees. 0 °corresponds to the exact north direction and 90° to the exact east direction.

With the use of the smartphone and compass app, the task can be solved quickly and accurately. Without compass, creativity is required. The direction could be determined by means of the position of the sun or the north directed mathtrail map. If it is clear that students should work without a compass, it makes sense to limit the question to the direction of the compass with multiple choice

Task of the Week: Vertebra

The city center of Münster provides several different tasks as one can notice within the portal map. Also in the trail around the Aasee, Münster presents itself from a various mathematical side. Aufgabe: Vertebra (Task Number: 4096). The work of art by Henry Moore created in 1974 represents several idealized vertebrae. These vertebrae are deliberately […]

The city center of Münster provides several different tasks as one can notice within the portal map. Also in the trail around the Aasee, Münster presents itself from a various mathematical side.

Aufgabe: Vertebra (Task Number: 4096).

The work of art by Henry Moore created in 1974 represents several idealized vertebrae. These vertebrae are deliberately close, yet unconnected to each other. Imagine, they were being put together and seen as part of an adult’s human spine. In reality, an average vertebra of a 1.80 m adult is about 2 cm long. Guess how big a giant would be whose spine would consist of vertebrae of this size (in m).

In this task, especially estimation and modelling are forced. Through the detail on the relation of body size and size of a human vertebra in the task, the size of the vertebra can be determined as an object of reference. An adequate measurement and calculation by means of the realtion results the questioned size.

Task of the Week: Height of the Statue

At the beginning of the month, Iwan Gurjanow presented the MathCityMap project in Sweden at the PME conference. Of course, around the location, different tasks were created as our current Task of the Week. Task: Height of the Statue (Task Number: 4303) How high is this statue? Give the result in meters. The task can […]

At the beginning of the month, Iwan Gurjanow presented the MathCityMap project in Sweden at the PME conference. Of course, around the location, different tasks were created as our current Task of the Week.

Task: Height of the Statue (Task Number: 4303)

How high is this statue? Give the result in meters.

The task can be solved via different approaches. On the one hand, it is possible to estimate how often a person with a known height fits into the heigth of the statue.

A more elaborated approach is the application of the intercept theorem, which is shown in the hint picutre. One can use the folding ruler as object of reference.

Task of the Week: Columns in the Parc

This week, Carmen Monzo, teacher in Spain gives us an inside into her task “Colums in the Parc”. It is created in a parc in Albacete, which ” is full of mathematical elements, though people are not aware of them until they are in math-vision mode.” Task: Columns in the Parc (Task Number: 3981) Calculate […]

This week, Carmen Monzo, teacher in Spain gives us an inside into her task “Colums in the Parc”. It is created in a parc in Albacete, which ” is full of mathematical elements, though people are not aware of them until they are in math-vision mode.”

Task: Columns in the Parc (Task Number: 3981)

Calculate the lateral surface (in m²) of one of the columns of this structure.

“I especially love this structure. Parallel and perpendicular lines can be easily identified, as well as a set of columns (cylinders) whose lateral surface can be easily calculated by using a folding ruler or a measuring tape, and a calculator to introduce the data and the formula. The height of the cylinder is easy to get, but to calculate the radius of the base as accurate as posible, students first have to measure the circumference and then divide by 2*pi.

As this structure has a dozen columns, the activity can be done by around 20 students, comparing their results and thinking about the importance of the accuracy when measuring. To solve this task, students should have previously studied 2D and 3D shapes, the concept of the lateral surface and some formula to calculate it.

As a secondary mathematics teacher, I think that our students need to handle things, measure, count, touch, feel, use their senses… MathCityMap provides the motivation students and teachers need to do those things with the help of the mobilephone technology.”

Task of the Week: Man walking to the Sky

This week, we focus on a task that can be used to realize linear functions in the environment. It was created by Kim Biedebach in Kassel. I became aware of MathCityMap during a didactics lecture as part of my teaching studies that I attended. The idea for the task actually came to me by chance. […]

This week, we focus on a task that can be used to realize linear functions in the environment. It was created by Kim Biedebach in Kassel.

I became aware of MathCityMap during a didactics lecture as part of my teaching studies that I attended. The idea for the task actually came to me by chance. I am from Kassel and had in mind that I have to design a modelling task for the lecutre. When I passed the figure, I spontaneously decided that this might be a suitable task.

Task: Man walking to the Sky (Task Number 3832)

How many meters is the man on the pole above the ground?

For this, the pole on which the man steps up is interpreted as a linear function. The point at which the pole starts on the ground is chosen as point (0, 0) for the sake of simplicity. Now, the slope must be determined as the quotient of the change in vertical and the change in the horizontal. If one starts from the chosen origin, and walks e.g.one meter to the side and measures the height there, the slope can be determined.

Afterwards, the slope can be used to determine the equation of function. Then the distance from the origin to the human on the ground has to be determined (corresponds to the x-coordinate). This is best done by positioning oneself under the man and measuring the distance to the origin. By inserting into the function equation the height can be calculated.

The task makes the linear relationship of x and y coordinates particularly clear. Also the slope concept is discussed. Of course, alternative approaches can be chosen, such as using the intercept theorems.

Task of the Week: Distance

During May, the MathCityMap Team created a trail in Zaryadye Parc in Moscow – in good time for the start of FIFA World Cup in June! One of the included tasks is in the focus of the “Task of the Week”, not at the latest through the object’s impressive architecture. Task: Distance (Aufgabennummer 3761) Calculate […]

During May, the MathCityMap Team created a trail in Zaryadye Parc in Moscow – in good time for the start of FIFA World Cup in June!

One of the included tasks is in the focus of the “Task of the Week”, not at the latest through the object’s impressive architecture.

Task: Distance (Aufgabennummer 3761)

Calculate the distance between the crosses at the top of the towers! Give the result in meters.

Already in the picture, it becomes obvious that the distance cannot be measured directly. Without the use of special measuring equipment, the task solvers have to develop a creative idea: The distance in the height can be projected on the ground.

This happens best through marked points at the building, or as shown in the picture from a certain distance. With this idea, the beginning problem of the height of the building can be avoided and the task can be solved easily.