circle | MathCityMap

2021-03-14: International Day of Mathematics with MCM@home

March 14 is International Day of Mathematics (IDM) – and MathCityMap is there, too, of course! Our MCM educator Simone has created a great MCM@home trail. We look forward to your participation! A truly well-rounded event! The MathCityMap@home-Trail makes clear in which objects mathematics – especially circles and the number Pi – can be found. […]

March 14 is International Day of Mathematics (IDM) – and MathCityMap is there, too, of course! Our MCM educator Simone has created a great MCM@home trail. We look forward to your participation!

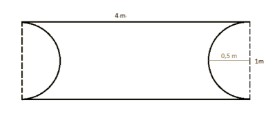
A truly well-rounded event! The MathCityMap@home-Trail makes clear in which objects mathematics – especially circles and the number Pi – can be found. The mathematical walk takes place in a different way than usual from home. Nevertheless, there is a lot to discover and calculate!

All you need to do is download the MathCityMap app. You can access the trail by adding routes and entering the given code. MCM users around the world were engaged in creating MCM@home trails for International Day of Mathematics (Pi Day):

Simone Jablonski created a MCM@home trail in Germany. The Digital Classroom can be invoked by entering the code s161437. Participation is possible between 0 and 23:55.
In Italy, Flavia Mammana and Eugenia Taranto prepared two MCM@home trail. With the code (044258) you can work on the trail for lower secondary students. The second trail (code 184244) treats topics on upper secondary level.
In Slovakia, Sona Ceretkova created the digital learning trail “[MCM@home]Pi-Nitra.” This can be accessed with the code 084229.
In Indonesia, Adi Nur Cahyono has prepared an MCM@home trail, which can be worked on today with the code s281455 as part of a digital classroom.

Task of the Week: The Ring

Dominik Enders, a student of the German grammer school (Gymnasium) in Bad Neustadt, created our new Task of the Week (the task “Ring”). In the interview, he explains why the students at his school create their own MCM tasks. How do you use MCM and why? I participate in a project, led by teacher […]

Dominik Enders, a student of the German grammer school (Gymnasium) in Bad Neustadt, created our new Task of the Week (the task “Ring”). In the interview, he explains why the students at his school create their own MCM tasks.

How do you use MCM and why?

I participate in a project, led by teacher Ms Gleichmann, in which we create math trails for pupils from younger classes, which you can tackle in your free time or on hiking days.

Describe your task. How can it be solved?

My problem is about a ring-shaped piece of sports equipment on a playground, of which you are supposed to find the area of the upper side. Assume that the edges of the ring are smooth, i.e. without indentations.

First you have to calculate the area of the circle up to the outer edge of the ring (tape measure/inch stick and pocket calculator are required) by determining the radius and then
calculate the area of the circle. Using the same procedure, calculate the smaller area of the circle enclosed by the inner edge of the ring. Then you only have to subtract the smaller area from the larger one to get the area of the top of the ring.

What didactic goals do you pursue with the task?

The task refers to the teaching content of the 8th grade and represents an application of the pupils’ knowledge on the topic of the area of a circle. The circle-ring is more demanding, but this can be mastered by using the area formula for two circles. The reference of mathematics in the 8th grade to a piece of sports equipment on a playground, which the pupils know from their everyday experience, should be motivating. By measuring lengths (radii), the topic of sizes from Year 5 is also addressed, as well as the importance of measuring accuracy.

Note: The task “Shoe size of the statue” was also created by a pupil of the Rhön-Gymnasium. It was the 15,000th task at MCM – great!

Task of the Week: Hercules Fountain

Our new Task of the Week is located in Montesarchio, an Italian town near Naples. Here, the math teacher Angela Fuggi created the task “Hercules Fountain”. In the interview, she presents her task and gives us an insight in the ERASMUS+ programme “Maths Everywhere”. How did you get to know MathCityMap? In this last […]

Our new Task of the Week is located in Montesarchio, an Italian town near Naples. Here, the math teacher Angela Fuggi created the task “Hercules Fountain”. In the interview, she presents her task and gives us an insight in the ERASMUS+ programme “Maths Everywhere”.

How did you get to know MathCityMap?

In this last school year I participated in the Erasmus project “ERASMUS + Maths Everywhere”. From 16th to 22nd February my school, the Istituto di Istruzione Superiore “E.Fermi” in Montesarchio (Benevento, Campania, Italy) hosted a group of 10 teachers and 29 students from Greece, Latvia, Spain and Turkey.

The focus of the project meeting in Montesarchio was “Math in the street”. Mathematics was viewed in close connection with the geographical area and its artistic and cultural heritage. One of the main activities was a treasure hunt and it was at this moment that MathCityMap came into play. The path created with the related activities had to be loaded onto MathCityMap and for this reason I started to use the app.

Please describe your task. How could you solve it?

My task related to the fountain located in the main square of Montesarchio. The artistic work, dating back to the second half of the 19th century, consists of a circular base with a basin, surmounted by a sculptural group of four lions and on a podium the figure of the warrior Hercules, the same mythical character who also appears on the emblem of the municipality. The task formulation is as follows:

In Umberto I square (the most famous square in Montesarchio) there is a fountain with 4 lions that surround Hercules, the Olympian god. The 4 lions are arranged at the vertices of a square on the side L. The statue of Hercules is supported by a circular base placed above the lions. Seen from above, this base is inscribed in the square with the 4 lions at the top. After measuring the distance between two consecutive lions, and therefore the side of the square, calculate the area of the circular base that supports the statue of Hercules (m²).

How could you solve it? Which is the didactic aim of this task?

The distance between two consecutive lions is the side of square L=2m. The side of the square coincides with the diameter D of the inscribed circumference, L = D, D=2m. The area of the circumference is A=π⋅(D:2)²=π⋅(2:2)²≈3,14 m²

The didactic aims were to represent, compare and analyze geometric figures and to work with them, identifying variations, invariants and relationships, above all starting from real contexts.

Task of the Week: Age of the Tree

“How old is this tree?” is the question of our current Task of the Week, which is located in Karlsruhe, Germany. Matthias Ludwig, the head of the MathCityMap team at Goethe University Frankfurt, gave us an interview about this task type. Please describe this task type. How the age of the tree could be ascertained? […]

“How old is this tree?” is the question of our current Task of the Week, which is located in Karlsruhe, Germany. Matthias Ludwig, the head of the MathCityMap team at Goethe University Frankfurt, gave us an interview about this task type.

Please describe this task type. How the age of the tree could be ascertained?

The task type “Age of the Tree” connects the learning of mathematics with non-mathematical knowledge or more specifically with information about trees: What does an oak, a beech or a lime tree looks like? How fast the tree species grows? Lots of further botanic questions could be examined subsequent to this task.

The classic solution process is to measure the circumference of the tree trunk at first, followed by the calculation of its diameter. However, students can also solve this task, if they don´t know the formula for the circumference yet. They can ascertain the diameter of the tree by measuring the distance between two parallel lines, which are both tangent to the trunk. If the students determined the diameter on one way or the other, they can approximate the age of the tree for example by using the rule of three.

The task “Age of the Tree” became a part of our task wizard a few weeks ago. The wizard provides all users prepared MathCityMap tasks, which can be created only by adding the measured data and a photo of the object – the sample solution and the hints emerge as if by magic.

Which didactic aims do you want to encourage through this task type?

In my opinion teachers and students should discover tasks, which exalt their mathematical imagination. For the reason that outdoor learning is highly useful, MathCityMap is one of many interesting ideas for the further development of modern math class.

Task of the Week: Flower Frame

Todays´ task of the week was created in Druskininkai, Lithuania, by our MoMaTrE project partner Sona Ceretkova. The aim of the task is to explore a flower frame and to calculate the missing percentage of the frame. Sona Ceretkova gave us an interview about this interesting task. What´s the topic of the task? The frame […]

Todays´ task of the week was created in Druskininkai, Lithuania, by our MoMaTrE project partner Sona Ceretkova. The aim of the task is to explore a flower frame and to calculate the missing percentage of the frame. Sona Ceretkova gave us an interview about this interesting task.

What´s the topic of the task?

The frame for the task is situated in Lithuania, spa town Druskininkai, which is flowers paradise itself. It is quite common gardening practice to frame a piece of lawn by stones or bricks and plant some nice composition of flowers inside the area of the frame. The flower frame chosen for the task is an interesting geometrical shape. rectangle with shorten sides cut.

Several mathematics calculations can be presented of the flower frame:

Calculate the inner area of the complete frame (without cuts).
Calculate the area of cut parts.
Calculate the difference between the area of the whole frame and cut parts.
Calculate the ratio of whole frame and cut parts.
Calculate the ratio of the cut frame and cut parts.
Calculate the missing percentage of the whole frame.
This is the given task in Druskininkai.

How could you solve this problem?

The original frame has “mathematically friendly” measures with a length of 4 metres and a width of 1 meter. The cut parts are two identical semi-discs, which create one whole disc (in calculation). This information is given by a hint. The geometrical situation of the task is quite simple (see figure).

Another hint declares that the area of the whole rectangle is 100%. This hint is an important note for correct calculation of the percentages. Since the exact percentage calculation gives 19,625%, rounding of this number was other mathematical skill required by solvers.

The multiple choice is the most suitable alternative as the answer. It´s an interesting game to ask solvers about their estimation of the tasks` solution. The 20% (one fifth) is a quite large number, quite large part, which is cut of the whole area of the flower frame. It is not so obvious when observing and measuring the real object.

What´s the didactic aim of the task?

We want to stimulate the following didactics aims through the task.

Measure precisely.
Imagine, draw or describe an ideal geometrical situation: rectangle, semi-circle (semi-disc).
Calculate areas of two basic geometric shapes: rectangle and circle (disc).
Use units in correct way; square meters are recommended.
Calculate number of percentages when knowing the base and the percentage part.
Interdisciplinary approach: ecology & botany

Task of the Week: Circular Ring

Today’s Task of the Week focuses on the circular ring. The idea behind is to determine the desired surface area by the difference of two surfaces, which can be calculated easily. Task: Ciruclar Ring (Task number: 1943) Calculate the area of the circular ring. Give the result in cm². The area of the circular ring […]

Today’s Task of the Week focuses on the circular ring. The idea behind is to determine the desired surface area by the difference of two surfaces, which can be calculated easily.

Task: Ciruclar Ring (Task number: 1943)

Calculate the area of the circular ring. Give the result in cm².

The area of the circular ring can be calculated by determining the radius of the entire circle, as well as the radius of the small “missing” circle. In this case, the easiest way is to measure the diameters of both circles. Then one calculates the wanted area either with the formula of the area of the circular ring, or one calculates the area of the entire circle and deducts the small circular gap. In both cases, the wanted area results.

A similar task can be created by means of traffic signs, e.g. the passage prohibited sign and the question of the proportion of red color. In both cases, the circle plays a thematic main role, so that the topic can be used from class 9 onwards.

Generic Tasks: Determining Quantities and Numbers

Determine quantities and numbers – an issue that is already relevant at primary level. For getting started in determining numbers, one should use regularly arranged objects like windows on a (high-rise) building, paving stones on a sideway or stones at a wall. When determining windows on houses, in many cases you can count the […]

Determine quantities and numbers – an issue that is already relevant at primary level. For getting started in determining numbers, one should use regularly arranged objects like windows on a (high-rise) building, paving stones on a sideway or stones at a wall.

Determine the number of windows on the house

When determining windows on houses, in many cases you can count the number of windows per row and the number of rows and get the result by multiplication. It is important to make clear whether you ask for windows or window panes, and whether all the windows of the building are relevant or, for example, only windows on the southern front.

Determine number of bricks

For walls and rectangular pavings there are several possibilities:

1. One determines the number n of the stones per 1m² and projects that to the total area A.

2. The length and height of the wall are determined in “stone units” and one counts the number of stones in length l and in width b.

Circular arranged stones with a gap

The level of difficulty increases when deviating from rectangular areas and e.g. asking for circular arranged stones. In addition, it can be difficult to determine the number of objects in which the regularity is interrupted in some places and one is forced to choose special solution methods.

You will find a detailed overview of our generic tasks on Determining quantities in the deposited PDF document.

Happy Pi Day

Friends of special dates and numbers might already have noted it in their calendar: Today is Pi Day. Based on the American spelling of today’s date (3/14) and the beginning of the number Pi with its first two decimals, the 14th March is perfect to celebrate Pi. Therefore, today everything at MCM revolves around the […]

Friends of special dates and numbers might already have noted it in their calendar: Today is Pi Day. Based on the American spelling of today’s date (3/14) and the beginning of the number Pi with its first two decimals, the 14th March is perfect to celebrate Pi. Therefore, today everything at MCM revolves around the circle and we would like to celebrate this with the help of one of our various tasks on the topic of the circle.

Task: Paving stones in a circle (Task number: 2007)

How many paving stones are in the red marked area?

Despite various approaches, the number Pi is central while solving the problem. On the one hand, it is possible to determine the number of paving stones in a certain area (for example one square meter) and to project them to the total area. The task can be solved particularly clever by considering a paving stone as a unit and expressing the radius of the circle by the number of stones.

This is just as one example of many tasks in which the number Pi is relevant in everyday life and for the math trail idea (e.g. traffic signs, advertising pillars, trees). In this sense: Happy Pi day!

By the way: the task is part of a trail around the Stuttgart’s stock exchange. They were created by our team and will be officially opened in April.

Task of the Week: Brick in the Wall

As a part of a teacher training at the Johanneum Gymnasium Herborn, a modeling task was created, which we would like to present to you today as the “Task of the Week”. Task: Brick in the Wall (task number: 2040) The wall in the schoolyard should be sprayed. It is planned to save color for […]

As a part of a teacher training at the Johanneum Gymnasium Herborn, a modeling task was created, which we would like to present to you today as the “Task of the Week”.

Task: Brick in the Wall (task number: 2040)

The wall in the schoolyard should be sprayed. It is planned to save color for the hole in the wall. Calculate the area to be sprayed in m². Enter the result with two digits.

The challenge in this task is to approach the existing hole in the rectangular wall as precisely as possible. Different models can be chosen for this purpose. On the one hand, one could assume the hole as a circle and determine an average diameter. More precisely, however, the result is obtained by approaching the hole as an ellipse and measuring the axes.

The task requires a certain amount of creativity and shows that the clear mathematics in the environment outside the classroom reaches its limits. The pupils acquire modeling competences, especially in the skillful choice of a mathematical model. The various solutions and results of the pupils thus form an ideal basis for discussing appropriate models. The problem can be applied with the treatment of circle and ellipse from class 9 onwards.

Task of the Week: Spider Web

While searching for suitable MathCityMap tasks, creativity and a focus for mathematics in the environment are required. This is also shown by the current Task of the Week, created by Stefan Rieger, in which a climbing frame is converted into a math task. Task: Spider web (task number: 1662) How many meters of rope does […]

While searching for suitable MathCityMap tasks, creativity and a focus for mathematics in the environment are required. This is also shown by the current Task of the Week, created by Stefan Rieger, in which a climbing frame is converted into a math task.

Task: Spider web (task number: 1662)

How many meters of rope does this spider web consist of?

Thankfully Mr. Rieger was available for a short interview, so he could give an insight into the idea behind the task.

How did you get the idea to create this task for MathCityMap?

Three of us were walking around the schoolyard, looking for interesting tasks. This task offered itself directly, because it is challenging and can be solved by younger students.

What competencies and topics play a role in the problem solving?

Here, it will be important that the group works together when it tries to solve the task. There are several people needed for measuring and recording. Accurate measurement and safe handling of the measuring tape will be necessary to solve the problem. Since it is intended as a task for the grades 5/6, the measuring (here non-straight lines) will be relevant. Of course, older students can use knowledge from the circle calculation.

Have you tested the task with students or received other feedback on the task?

No. The task will be tested in the next school year with grade 5 as well as in the course of a further teacher training with colleagues. However, he climbing children had a lot of fun to help me as a climber for checking the measurements.

We are pleased that MathCityMap finds more and more task authors from different regions and the task portal is expanded by a variety of tasks!