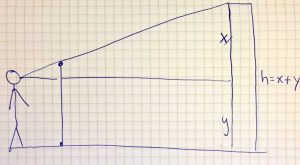
Fountains and their volume are ideal for modeling different geometric bodies. While many of the fountains have a rectangular or circular shape and can thus be approximated as cuboid or […]

As part of the ICM conference in Rio de Janeiro, Iwan Gurjanow created the first tasks in South America. In the resulting trail, our current Task of the Week is […]

With our GPS tasks, such as the walking of a north-south line, we have already presented a first way how to connect the directions with MathCityMap. But many statues also […]

Doing mathematics surrounded by a fantastic setting – that promises the current Task of the Week to the statue of Diogenes of Sinope. Known as an influential Greek philosopher, he […]

The city center of Münster provides several different tasks as one can notice within the portal map. Also in the trail around the Aasee, Münster presents itself from a various […]

At the beginning of the month, Iwan Gurjanow presented the MathCityMap project in Sweden at the PME conference. Of course, around the location, different tasks were created as our current […]

This week, Carmen Monzo, teacher in Spain gives us an inside into her task “Colums in the Parc”. It is created in a parc in Albacete, which ” is full […]

The classical geometric bodies and figures can be found numerously in the environment. However, real objects deviate from the ideal body and require modeling skills. In addition, composite bodies are […]

On June, 15th and 16th, the MoMaTrE partners from Frankfurt und Spain met in Alcala de Henares near Madrid  in order to fix aims and tasks for the project. In […]

This week, we focus on a task that can be used to realize linear functions in the environment. It was created by Kim Biedebach in Kassel. I became aware of […]