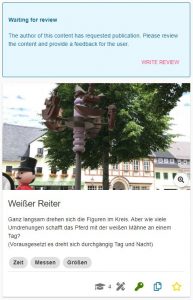
The trail of the month September comes from Switzerland. Here, primary school teacher Roger Pellaton created the “Skulpturenweg Leywald Reinach” which can be accessed via MCM app using the code 384906. It is available on the web portal here.
There are a total of twelve tasks on this math trail, most of which were designed directly on the trail’s magnificent wooden sculptures.
How did you come across the MathCityMap project?
I’ve worked with Actionbound before, and even earlier with GeoCaching. This year, students from the FHNW (University of Applied Sciences Northwestern Switzerland) are on a year-long internship at our school. The students were given the task of digitally implementing map work in a 6th grade class. From the FH they brought the hint MathCityMap, which was unknown to me until then, and they wanted to know from me what other alternatives there were. After a bit of exchange and joint evaluation, we decided to implement the project with MathCityMap. MCM was new to all of us, so we experimented a bit together and immediately documented our experiences for the rest of the college, so that other teachers could benefit from the preliminary work already done.
Please describe your Mathtrail.
The sculpture trail in Reinach is well-known all around. Most of the children already knew it when I tried this trail with them. They were already there in kindergarten, most likely in junior high school, and with their parents often as well. Nevertheless, they see it with completely different eyes when they have to solve a very specific math problem at a certain sculpture. In the middle of the forest! The device in their hand gives them additional feedback as to whether they have solved the task correctly. You can’t get any further away from the classroom than being in the forest, surrounded by artistically carved wooden figures that exude a peculiar calm and fascination. What’s more, with a trail like this, you’re not only carrying the math out of the classroom, you’re also carrying it right into the parents’ home when the next walk-through involves the parents.
How do you use MCM and why?
At our school, all middle school students (4th/5th/6th grades) are equipped with iPads in ascending order. We started with the 4th graders this year, and the new 4th graders will join them after the summer vacations. As a class teacher of such a class, I also accompany the entire IT project at our school on the pedagogical side. This is called PICTS (Pedagogical IT Support). As PICTS, one of my tasks is to show the teachers ways in which they can use the iPads of their class profitably in the classroom. So I visualize such tools and projects on an ongoing basis, trying out much of these in my own class first, then bringing them back to my colleagues.
Since I consider self-directed interpretation of assignments and tasks to be one of the most central key competencies of modern life, I am grateful for tools such as MCM that allow my students to have experiences that are highly effective for learning in a protected setting. The fact that Corona, Lockdown, and distance learning have given IT a noticeable boost on the one hand is great, but on the other hand this crises shrinks the world of children to an unpleasantly small 13 inches, which does not make me happy. MCM starts exactly there and puts math tasks outside the classroom into a new context. I liked that, and unsurprisingly, so did my students.
Describe your favorite task of the trail. How can this be solved?
I don’t really have a “favorite” task. I generally like tasks that hold something surprising, or open a previously closed door. The Snow White task, for example, where the children have to put themselves in the dwarves’ shoes and figure out which dwarf can see which other dwarf or not, that’s one such task. Or when, during the task with the “Gluggerbahn” (Glugger = Swiss German for marble), they suddenly find out what the piece of string is for that they were supposed to stuff into their pockets at the beginning of the trail. Sometimes, as a teacher, you are lucky enough to be present at such moments.