Simone Jablonski | MathCityMap

Task of the Week: Number of Windows

While during the past few weeks we often presented tasks which can be solved from secondary level, the present Task of the Week shows that the MathCityMap project can already be used from primary school. Task: Number of Windows (task number: 1191) How many window panes can be seen on this front of the house? To solve the […]

While during the past few weeks we often presented tasks which can be solved from secondary level, the present Task of the Week shows that the MathCityMap project can already be used from primary school.

Task: Number of Windows (task number: 1191)

How many window panes can be seen on this front of the house?

To solve the problem, it is possible to count the window panes. However, this takes a long time so that the students at best have the idea to count only the panes in a row as well as the number of rows and solve the task by means of a multiplication. The basic representation of the multiplication is addressed as a repeated addition. Further, the students must be aware that the number of window panes and not the windows is asked. For a window, therefore, three panes must be submitted if the students firstly count the number of windows.

The task can be classified in the areas of multiplication and number and can be solved from class 4.

Task of the Week: Pavilion

The present task of the week is about a geometric question. It involves the area calculation of the roof surface of the illustrated pavilion. Task: Pavilion (task number: 665) Determine the roof surface of the pavilion! Give the result in m². For this purpose, the pupils should recognize that the roof surface consists of several isosceles […]

The present task of the week is about a geometric question. It involves the area calculation of the roof surface of the illustrated pavilion.

Task: Pavilion (task number: 665)

Determine the roof surface of the pavilion! Give the result in m².

For this purpose, the pupils should recognize that the roof surface consists of several isosceles triangles. It is therefore sufficient to measure the height and base of one triangle and to calculate the surface content using the formula for the area content of triangles. The total area can then be determined by multiplication by the number of triangles.

In order to solve the problem, the pupils must therefore be familiar with the area calculation for triangles. In the task, the “geometrical view” is trained by the triangular shape being recognized in a composite figure. Here, an essential aspect of outdoor mathematics is found, namely the recognition of mathematical concepts and objects in reality, as well as the use of mathematical knowledge to solve everyday questions. Solving the task is possible from class 6 onwards with the topic triangles.

After our presentation in Münster at the beginning of the week, the WDR created a short video about our MCM app. A student tested the trail in Münster and did quite well.

Have fun watching. Click here for the video.

MCM in Münster at the Aasee

On Tuesday, 23.05.2017, members of the MCM team were invited by the research team of the University of Münster to create a Math Trail in the north of the Aasee. They also informed interested teachers about the basic didactic theories as well as the technical possibilities of the MCM project. 28 teachers and interested people followed the invitation and, according […]

On Tuesday, 23.05.2017, members of the MCM team were invited by the research team of the University of Münster to create a Math Trail in the north of the Aasee. They also informed interested teachers about the basic didactic theories as well as the technical possibilities of the MCM project. 28 teachers and interested people followed the invitation and, according to the theory, tested the app and the tasks of the route Aasee Nord.

MathCityMap – Reloaded

On Thursday, 24 participants took part in the House of Finance at the Westend Campus of the Goethe University and wanted to find out about the latest developments in the MathCityMap project. The entire MCM team was present, so that the information could be given first-hand. Matthias Ludwig presented how the MCM project is genetically […]

On Thursday, 24 participants took part in the House of Finance at the Westend Campus of the Goethe University and wanted to find out about the latest developments in the MathCityMap project. The entire MCM team was present, so that the information could be given first-hand.

Matthias Ludwig presented how the MCM project is genetically integrated into the math-out-of-nature-concept of MATIS I scientifically and didactically. In this concept the authenticity aspect, the influence of physicality, the psychology of emotions and interest, as well as the life environment are taken into account by new technologies, as well as the sharing idea that leads to an exchange among the participating teachers. Joerg Zender introduced the application of the app (now also as an iOS version) before the participants solved tasks from the Westend Trail with folding rule and measuring tape. After 50 minutes, Martin Lipinski moderated the discussion on the first experiences with the trail and presented the MCM criteria for a good task. Afterwards, a second practice part took place, in which the participants developed their own task. Iwan Gurjanow, who is responsible for the programming of the MCM app and the MCM portal, took the final step. He explained how to integrate one’s own tasks, combine them to a route and create a group.

The participants did not want to go home, but wanted to work on their MCM tasks even longer. Do not worry next year, we’ll be back with an 4 hours event!

Task of the Week: Passage prohibited

The current “Task of the Week” shows that many geometrical questions can be found in different traffic signs. This concerns the circular “passage prohibited” sign and, in particular, the question of the ratio of red and white surfaces. Task: Passage prohibited (task number: 1102) How many percent of the area of the “passage prohibited” sign is red? […]

The current “Task of the Week” shows that many geometrical questions can be found in different traffic signs. This concerns the circular “passage prohibited” sign and, in particular, the question of the ratio of red and white surfaces.

Task: Passage prohibited (task number: 1102)

How many percent of the area of the “passage prohibited” sign is red?

For the calculation, the pupils have to use their knowledge about the area of the circle. In addition, it must be noted that the shield is not only white on the inside, but has a white edge as well, which must be considered for an exact calculation. The pupils measure the different radii, calculate the total area and the area of the two white surfaces. By means of subtraction the surface content of the red ring is obtained. In the last step, the percentage of the red area has to be calculated.

The task can be classified in the area of geometry, more specifically in circles and area contents, and is releasable from class 7 onwards. Other traffic signs can be integrated in a similar way into geometric questions, such as the “entrance prohibited” sign on a one-way street. In particular, the different flat figures on street signs (circle, triangle, rectangle, octagon) motivate different tasks.

Task of the Week: Combinatorical Stair

The focus of today’s Task of the Week is a combinatorial question. In addition to the typical combinatorical question for the number of possibilities, an application of the Fibonacci numbers, which can be discovered by the students, is included as well. Task: Combine Staircase (task number: 1199) How many options are available to climb the stairs […]

The focus of today’s Task of the Week is a combinatorial question. In addition to the typical combinatorical question for the number of possibilities, an application of the Fibonacci numbers, which can be discovered by the students, is included as well.

Task: Combine Staircase (task number: 1199)

How many options are available to climb the stairs by climbing one or two steps per step? The steps can also be combined.

There are various possibilities for solving the problem. On the one hand, it is possible to systematically record different combinations of 1 and 2 steps. In doing so, the students can use the stairs directly and conclude which combinations are possible. In another consideration, the fact that the last step comprises either one step or two steps is used. Leaving this last step, the number of possibilities for a staircase with n steps can be determined using the possibilities for n-1 and n-2 steps. This reasoning leads to the Fibonacci numbers, a recursive sequence in which a number results from the addition of its two predecessors.

The task is therefore a successful example of “hidden” mathematics in simple everyday objects. It offers the possibility to go deeper into the topic Fibonacci numbers or to let the students discover them. At the same time, the problem can also be solved by systematic testing, so that it can be used from class 6. Its topic belongs to combinatorics.

Create Tasks magically – The Task Wizard is online!

It has been a bit longer since there was a bigger update of the MCM web portal. But now it is time and it brings two major innovations with it. Task Wizard The Task Wizard allows you to create complete tasks with a few clicks. The author has to find a suitable object in his environment, take a picture […]

It has been a bit longer since there was a bigger update of the MCM web portal. But now it is time and it brings two major innovations with it.

Task Wizard

The Task Wizard allows you to create complete tasks with a few clicks. The author has to find a suitable object in his environment, take a picture of it and collect the necessary measurement data. The remaining entries, such as the sample solution and notes, are automatically generated and inserted by the wizard. At first, a set of 12 task templates from the topics slope, number, volume / weight and combinatorics are available. The templates originate from our collection of blueprint tasks and can be formulated on objects which, according to experience, occur almost everywhere:

• Handrail of a Staircase

• Ramp

• Stone Wall

• Paving Stones

• Advertising Pillar

• Large Stones

• Wooden Trunk

• Water basin / fountain.

The task wizard will be expanded step by step. Suggestions for new task templates from the community are gladly taken up! To start the wizard, you just have to click on “New Task” in the portal, then select the magic wand and afterwards you can start.

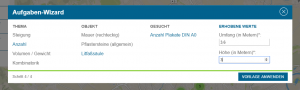
For a time-consuming, but still good trail, we recommend about 5 own tasks, which are individual and unique for the place, mixed with 5 tasks from the task wizard.

Quality Traffic Light

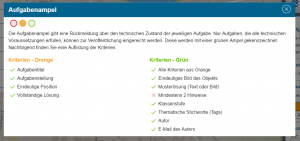
Tasks and routes now have a so-called “Quality Traffic Light” which reflects the technical quality of the element. The traffic light is located in the area where the picture is displayed. By clicking on the traffic light, you can see which criteria are already fulfilled and which can be improved. To ensure that our public tasks and trails continue to be of a high quality, only tasks and routes that show the green light can be submitted for publication.

Further changes:

• In the route view, the path within the route is also displayed. The starting task is marked with a blue circle.

• Tasks can now be added / removed to a route using a button (“Add / Remove”) in the task preview. This should facilitate routing.

• Quotation marks and line breaks in hints, sample solutions and task texts are now displayed correctly.

Task of the Week: Cylinder on the Rhine

The present task of the week is about geometric figures. In the task “Cylinder on the Rhine”, located in Cologne, the aim is to determine the radius of a cylinder by means of measurements or the relationship between radius and circumference of a circle. Task: Cylinder on the Rhine (task number: 1183) Determine the radius of […]

The present task of the week is about geometric figures. In the task “Cylinder on the Rhine”, located in Cologne, the aim is to determine the radius of a cylinder by means of measurements or the relationship between radius and circumference of a circle.

Task: Cylinder on the Rhine (task number: 1183)

Determine the radius of the cylinder. Give the result in m.

The task can be solved in different ways. One possibility is to use the relationship between the circumference of the circle and the diameter or radius. The result is then obtained by measuring the circumference. Alternatively, the radius can be determined by means of the inch post and suitable application (here the right angle plays a role). The task can therefore be classified into the topic circle, in particular the formula for the calculation of the circumference. The task shows that mathematical tasks can often be solved in various ways without calculation. Although the task does not require any profound knowledge of the cylinder (apart from the fact that the base is circular), it can be precisely in this aspect, and a connection of planar and spatial geometry can be made clear.

It can be used starting from class 9.

The present task of the week is about a sculpture in form of a hand. In this form, it can be found in the Dillfeld Trail in Wetzlar. The aim of the task is to determine the body size of the person to whom this hand would fit.

Task: The Hand (task number: 1092)

How big would a man be in meters with a hand of this size?

The pupils should measure a finger that is easily accessible to them. Especially the thumb offers itself for it. How can the thumb size be related to the body size? For conversion, the own body can play a role by correlating the thumb size and the body size. Then the body size of the human with the shown hand can be determined. The students use the idea of measuring their own body and the hand sculpture. In particular, relations and sizes play a role. The task can be used from class 6 on with the development of relations.

Author: Simone Jablonski