Adrian Schrock, math teacher at the Weibelfeldschule in Dreieich (Germany), has created our new Trail of the Month. The tasks of the math trail aim at the topics Theorem of Pythagoras and the Intercept Theorem. By this example we want to show how you can create so-called theme-based math trails with close curricular links. In this interview Adrian Schrock talks about his experiences with MathCityMap.
How do you use MCM and why? What is special about your trail?
I currently use the trail „Unseren Schulhof mit Mathe entdecken“ (engl.: “Discovering our schoolyard by doing maths”) in my 9th grade in the subject area “Pythagorean theorem” and ” Intercept theorems” and would like to increase the motivation for problem solving in class.
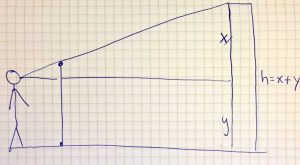
What is special about my trail is that all the tasks are in the schoolyard and combine the topics “Pythagorean theorem” and “Intercept theorems”. Not only inaccessible variables like the height of the school building can be calculated, but also by reversing the theorems both the 90° angle and the parallelism can be checked using objects in the schoolyard.
The first task is explicitly intended as an introduction to working with the Mathtrail and should be carried out in small groups in the classroom. I have already tested this successfully in class and had the advantage that the SuS first get to know the app and possible questions can be clarified directly in the plenum.
In order to increase the relevance of the tasks, a short story is formulated in my descriptions “About the object”, which shows why the question could be interesting. For example: “Between the columns a screen for a stage set can be hung up. A teacher wants to know for a performance of the Performing Play in an open-air theatre whether the screens are parallel to each other”. The stories are, of course, made up, but may answer the question of the students “Why would you want to know that?”.
What didactic goals do you pursue?
On the one hand, the trail aims to specifically promote motivation for problem solving in the 9th grade. On the other hand, by focusing on the selected topics, the trail has the additional purpose of being able to apply the teaching content to real objects and thus deepen the knowledge. The advantage of this is that it is clear from the starting situation of the SuS that previous knowledge is required for the trail. A disadvantage is, of course, that if you work on other class levels, your motivation might be lower, because you don’t see any connection to your current lessons.
Further remarks about MCM?
Small wish to the MCM team… the Task Wizard lacks task types to determine heights or to check for example parallelism or something similar to my trail. Maybe you could add some more topics here.
I find the structure of the website and especially the feedback to the created tasks very good – thanks a lot to the MCM team!