Aufgaben | MathCityMap

Die Aufgabenformate bei MathCityMap

Kürzlich haben wir mehrere neue Aufgabenformate entwickelt! MathCityMap bietet mittlerweile neun Aufgabenformate zuzüglich der Möglichkeit, Unteraufgaben zu komplexeren Aufgaben zu erstellen. Alle Aufgabenformate werden im Folgenden kurz vorgestellt. Außerdem stellen wir Ihnen einen Beispiel-Trail mit allen Aufgabenformaten zur Verfügung. Dieser Trail kann hier im Webportal bzw. über den Code 065522 in der MathCityMap-App angesehen werden. […]

Kürzlich haben wir mehrere neue Aufgabenformate entwickelt! MathCityMap bietet mittlerweile neun Aufgabenformate zuzüglich der Möglichkeit, Unteraufgaben zu komplexeren Aufgaben zu erstellen. Alle Aufgabenformate werden im Folgenden kurz vorgestellt.

Außerdem stellen wir Ihnen einen Beispiel-Trail mit allen Aufgabenformaten zur Verfügung. Dieser Trail kann hier im Webportal bzw. über den Code 065522 in der MathCityMap-App angesehen werden.

Das Intervall ist das „klassische“ MathCityMap-Aufgabenformat. Es sollte immer dann verwendet werden, wenn Messungen notwendig sind, z. B. um eine Länge, eine Fläche oder ein Volumen zu bestimmen.

Intervall

Das Format Exakter Wert kann für Zählaufgaben oder für kombinatorische Probleme verwendet werden: Wie viele Fenster erkennt man an der Hauswand? Wie viele Möglichkeiten habe ich, mein Fahrrad an diesem Fahrradständer abzuschließen?

Exakter Wert

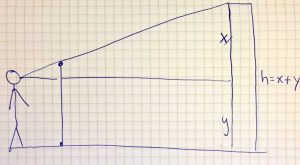
Um mehr als eine Frage zu einer Messaktivität zu stellen, kann das Aufgabenformat Vektor (Intervall) verwendet werden. Beispiel: Bestimmen Sie die Länge, Breite und Höhe des abgebildeten Quaders. Auch bei Fragen zur räumlichen Geometrie kann das Aufgabenformat angewendet werden.

Vektor (Intervall)

Neues Format!

Analog dazu bieten wir das Format Vektor (Exakter Wert) an, mit dem Sie mehrere Zählaufgaben oder kombinatorische Probleme auf einmal stellen können.

Vektor (Exakter Wert)

Neues Format!

Wenn mehrere Zahlen die erwartete Lösung in einer Aufgabe sind, aber die Reihenfolge, in welcher die Zahlen eingegeben werden sollen, nicht wichtig ist, kann das Aufgabenformat Menge genutzt werden. Ein Beispiel für eine Mengen-Aufgabe finden Sie im oben erwähnten Mathtrail.

Menge

Neues Format!

Die Informationsstation ist ein Aufgabenformat ohne Lösungsfeld. Hier können u.a. wichtige Fakten zu historischen Gebäuden, Personen oder Gegebenheiten während des Mathtrails vorzustellen.

Informationsstation

Neues Format!

Ein weiteres neues Aufgabenformat ist der Lückentext: Mit diesem Format können Lückentexte für das außerschulische Lernen entwickelt werden, z. B. um Fachsprache einzuüben, sich mit Daten von Informationstafeln auseinanderzusetzen oder Fragen zu Daten historischer Gegebenheiten zu stellen.
Hinweis: Bitte verwenden Sie den Modus „streng“, wenn eine Zahl in die Lücke eingetragen werden soll.

Lückentext

Neues Format!

Auch können vorhandene Daten im Multiple-Choice-Format wie in einem Quiz abgefragt werden. Dabei müssen mindestens zwei Antwortmöglichkeiten gegeben sein, von denen mindestens eine richtig ist.

Multiple Choice

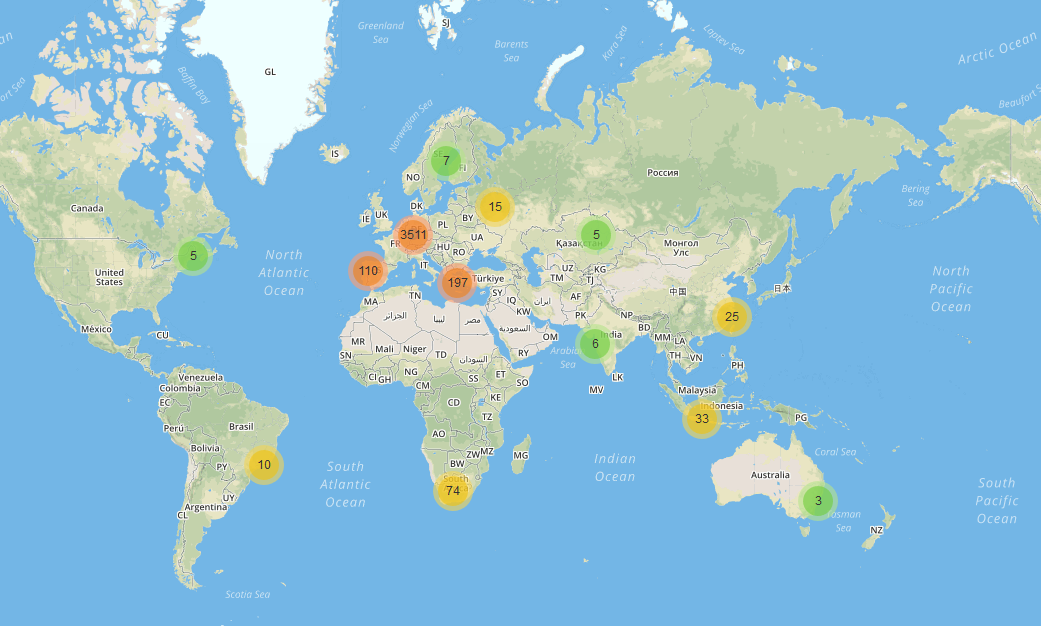
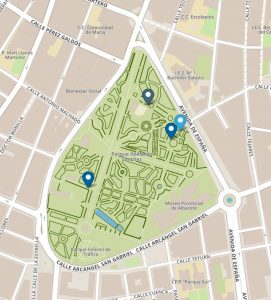
Mit dem GPS-Aufgabenformat können Sie Aufgaben erstellen, bei denen die Schüler eine vordefinierte Position finden müssen (z. B. die Mitte der vorgegebenen Punkte) oder sich in einer gegebenen Figur positionieren müssen (z. B. als Eckpunkte eines gleichseitigen Dreiecks)
Hinweis: Dieser Aufgabentyp funktioniert am besten in eher ländlichen Gebieten, da das GPS-Signal in Städten oft zu schwach ist.

GPS-Aufgabenformat

Schließlich bieten wir die Möglichkeit, komplexere Aufgaben vorzustrukturieren, indem sie in optionale oder obligatorische Unteraufgaben aufgeteilt werden. Ein Beispiel für die Verwendung von Unteraufgaben finden Sie in der oben genannten Strecke.

Unteraufgaben

Neues Format!

Projekt lässt Schüler zu Aufgabenerstellern werden

Im folgenden Interview mit Vera Korff wird ein Einblick in die Erstellung von MathCityMap Aufgaben mit Schülern in Bergisch Gladbach gegeben. Wir bedanken uns für das Interview und wünschen weiterhin viel Spaß mit MCM! Wie sind Sie auf MathCityMap aufmerksam geworden und in welchem Rahmen haben Sie es eingesetzt? Ich habe MathCityMap im Rahmen meines […]

Im folgenden Interview mit Vera Korff wird ein Einblick in die Erstellung von MathCityMap Aufgaben mit Schülern in Bergisch Gladbach gegeben. Wir bedanken uns für das Interview und wünschen weiterhin viel Spaß mit MCM!

Wie sind Sie auf MathCityMap aufmerksam geworden und in welchem Rahmen haben Sie es eingesetzt?

Ich habe MathCityMap im Rahmen meines Referendariats am Zentrum für schulpraktische Lehrerausbildung Köln kennengelernt. In einem Workshop wurde uns die App vorgestellt und wir durften sie auch selber ausprobieren, was unheimlich viel Spaß gemacht hat.

Da ich als „Anfängerin“ noch recht lange für die alltägliche Unterrichtsvorbereitung benötige, bin ich leider nicht dazu gekommen, die App im „normalen“ Unterricht einzusetzen. Ich packte jedoch die Gelegenheit am Schopfe, als an unserer Schule in der vorletzten Woche vor den Ferien eine Projektwoche veranstaltet wurde. Für den ersten Tag der Projektwoche habe ich mit einer Kollegin einen Trail um die Schule herum vorbereitet, damit die Projektteilnehmer (acht Schüler) die App und mögliche Aufgabenformate kennenlernen.

Anschließend gingen wir in die Bergisch Gladbacher Fußgängerzone, damit die Schüler Ideen und Informationen für einen eigenen Trail sammeln konnten. Am nächsten Tag wurden dann die Trails am PC zusammengestellt und im Anschluss von der jeweils anderen Gruppe ausprobiert. Die Trails wurden abschließend reflektiert und es wurde besprochen, welche Kriterien für eine „perfekte“ Aufgabe realisiert werden müssen.

Am letzten Tag haben die Schüler eine Powerpoint-Präsentation über MathCityMap sowie zwei „perfekte“ Aufgaben erstellt, um ihre Arbeit am Präsentationstag (einem Samstag) den Besuchern vorzustellen. So konnten die Besucher nach der Präsentation zusammen mit den Gruppenmitgliedern auf den Schulhof gehen und die Aufgaben selbst ausprobieren.

Reflexion des Projekts

In der Reflexion sagten die Schüler, dass ihnen das Erstellen der Aufgaben Spaß gemacht hat. So konnten sie Gegenstände, die sie tagtäglich sehen, einmal genauer und aus einem anderen Blickwinkel unter die Lupe nehmen.

Das Projekt zeigt demnach, dass Schüler nicht nur als Aufgabenlöser, sondern auch als Aufgabenersteller tätig werden können. Dennoch betont Vera Korff, die Notwendigkeit, bei technischen Schwierigkeiten und Fehlerberechnungen als Projektleiter zu unterstützen, sodass es nicht zu Frustration und Überforderung kommt.

4000. MathCityMap Aufgabe im Portal

Bei dem anhaltenden sommerlichen Wetter ist es eigentlich kein Wunder, dass es die Mathtrailer nach draußen zieht. Wir freuen uns besonders darüber, dass in dieser Woche die 4000-Aufgaben-Grenze im Portal überschritten wurde. Outdoor Mathematik mit MathCityMap rund um den Globus haben wir aktuell rund 1500 Usern zu verdanken. Zusammen wurden über 600 Routen in 17 […]

Bei dem anhaltenden sommerlichen Wetter ist es eigentlich kein Wunder, dass es die Mathtrailer nach draußen zieht. Wir freuen uns besonders darüber, dass in dieser Woche die 4000-Aufgaben-Grenze im Portal überschritten wurde.

Outdoor Mathematik mit MathCityMap rund um den Globus haben wir aktuell rund 1500 Usern zu verdanken. Zusammen wurden über 600 Routen in 17 verschiedenen Ländern angelegt. Beachtliche Anteile daran haben neben unseren internationalen Kooperationspartnern von MoMaTrE und dem MOOC der Universität Turin auch die vielen engagierten und motivierten Aufgabenersteller, die MathCityMap an ihrer Schule, Universität oder in ihrer Freizeit nutzen. An dieser Stelle vielen Dank!

Das Projekt hat damit eine wie wir finden tolle Entwicklung hingelegt und lässt uns bereits einige Zukunftspläne schmieden.

Aufgabe der Woche: Höhe der Skulptur

Zu Beginn des Monats hat Iwan Gurjanow das MathCityMap Projekt erfolgreich in Schweden auf der PME Konferenz vorgestellt. Natürlich wurden vor Ort auch Aufgaben angelegt, so wie die heutige Aufgabe der Woche. Aufgabe: Höhe der Statue (Aufgabennummer: 4303) Wie hoch ist die Statue? Gib das Ergebnis in Metern an. Die Aufgabe lässt sich auf verschiedene […]

Zu Beginn des Monats hat Iwan Gurjanow das MathCityMap Projekt erfolgreich in Schweden auf der PME Konferenz vorgestellt. Natürlich wurden vor Ort auch Aufgaben angelegt, so wie die heutige Aufgabe der Woche.

Aufgabe: Höhe der Statue (Aufgabennummer: 4303)

Wie hoch ist die Statue? Gib das Ergebnis in Metern an.

Die Aufgabe lässt sich auf verschiedene Arten lösen. Zum einen ist es aus einer größeren Entfernung möglich, mithilfe einer Person als Referenzgröße zu schätzen, wie oft diese Person in die Statue passt.

Genauer wird es, wenn die Aufgabe mithilfe des Strahlensatzes gelöst wird, wie im folgenden Hinweisbild dargestellt:

Als Referenz kann hier der Zollstock dienen.

Aufgabe der Woche: Säulen im Park

Diese Woche gibt uns Carmen Monzo, Lehrerin in Spanien, einen Einblick in ihre Aufgabe „Säulen im Park“. Die Aufgabe wurde in einem Park in Albacete erstellt, der „viele mathematische Elemente enthält, die die Leute nicht wahrnehmen, solange sie nicht die mathematische Brille aufhaben.“ Task: Säulen im Park (Task Number: 3981) Bestimme die Oberfläche (in m²) […]

Diese Woche gibt uns Carmen Monzo, Lehrerin in Spanien, einen Einblick in ihre Aufgabe „Säulen im Park“. Die Aufgabe wurde in einem Park in Albacete erstellt, der „viele mathematische Elemente enthält, die die Leute nicht wahrnehmen, solange sie nicht die mathematische Brille aufhaben.“

Task: Säulen im Park (Task Number: 3981)

Bestimme die Oberfläche (in m²) einer der Säulen.

„Ich mag insbesondere diese Stuktur. Parallele and senkrechte Linien können einfach gefunden werden, ebenso wie die Säulen (Zylinder), deren Oberfläche einfach mithilfe eines Zollstocks oder Maßbands und einem Taschenrechner bestimmt werden kann. Die Höhe des Zylinders kann einfach bestimmt werden, aber für eine möglichst genaue Bestimmung des Radius‘ am Boden, müssen die Schüler zunächst den Umfang messen und durch 2 Pi dividieren.

Da es zwölf Säulen gibt, can die Aufgabe simultan von etwa 20 Schülern bearbeitet werden. Anschließend können sie ihre Ergebnisse vergleichen und über die Wichtigkeit der Messgenauigkeit nachdenken. Um die Aufgabe zu lösen ist Wissen über 2D und 3D Formen, das Konzept der Oberfläche und Formeln zur Berechnung notwendig.

Als Sekundarstufen Mathematiklehrerin denke ich, dass unsere Schüler verschiedene Aktivitäten wie messen, zählen, fühlen und mit ihren Sinnen arbeiten durchführen sollten. MathCityMap gibt Schülern und Lehrern die Motivation solche Dinge mit moderner Smartphone Technologie zu betreiben.

MathCityMap auf dem New Horizons in Teaching Science Workshop in Italien

Am 18. Juni 2018, fand der the „New Horizons in Teaching Science“ in Messina auf Sizilien statt. Bei diesem Anlass stellte Eugenia Taranto das MathCityMap Projekt und die Kooperation mit dem Matheprojekt MOOC UniTo (Massive Open Online Course Universität Turin). Viele verschiedene Aufgaben, die im Rahmen des MOOC „Verhältnis und Funktionen“ von sizilianischen Lehrern erstellt […]

Am 18. Juni 2018, fand der the „New Horizons in Teaching Science“ in Messina auf Sizilien statt.

Bei diesem Anlass stellte Eugenia Taranto das MathCityMap Projekt und die Kooperation mit dem Matheprojekt MOOC UniTo (Massive Open Online Course Universität Turin).

Viele verschiedene Aufgaben, die im Rahmen des MOOC „Verhältnis und Funktionen“ von sizilianischen Lehrern erstellt wurden, konnten gezeigt werden.

Es zeigte sich vielseitiges Interesse und wir hoffen, dass die Zahl an sizilianischen und italienischen Aufgaben weiterhin wachsen wird!

Aufgabe der Woche: Abstand der Türme

Im Mai hat das MathCityMap Team einen Trail im Zaryadye Park in Moskau angelegt – rechtzeitig zum Start der Fußball WM im Juni! Eine der darin enthaltenen Aufgabe soll in dieser Woche im Fokus der Aufgabe der Woche stehen, nicht zuletzt aufgrund der beeindruckenden Architektur des Objekts. Aufgabe: Abstand der Türme (Aufgabennummer 3761) Bestimme den […]

Im Mai hat das MathCityMap Team einen Trail im Zaryadye Park in Moskau angelegt – rechtzeitig zum Start der Fußball WM im Juni!

Eine der darin enthaltenen Aufgabe soll in dieser Woche im Fokus der Aufgabe der Woche stehen, nicht zuletzt aufgrund der beeindruckenden Architektur des Objekts.

Aufgabe: Abstand der Türme (Aufgabennummer 3761)

Bestimme den Abstand zwischen den Kreuzen auf den Türmen. Gib das Ergebnis in Metern an.

Bereits in der Abbildung wird deutlich, dass die Strecke nicht direkt gemessen werden kann. Ohne die Verwendung von speziellem Messwerkzeug müssen die Aufgabenlöser eine kreative Idee entwickeln: Der Abstand in der Höhe lässt sich auf den Boden projizieren.

Dies geschieht am besten mithilfe von markanten Stellen am Gebäude, oder wie im Bild dargestellt aus einer gewissen Distanz. Mit dieser Idee lässt sich die anfängliche Hürde der Höhe des Gebäudes schnell umgehen und die Aufgabe einfach lösen.

Aufgabe der Woche: Blumentopf

Wenn Sie das MathCityMap Portal durchforsten, werden Sie feststellen, dass Blumentöpfe für vielfältige geometrische Aufgabenstellungen dienen. Alleine durch das häufige Vorkommen und die verschiedenen Formen (Zylinder, Prisma mit sechseckiger Grundfläche, etc.) wird die Fragestellung, wie viel Liter Erde in einen Blumentopf passen, realisiert. In der heutigen Aufgabe der Woche handelt es sich um einen Blumentopf […]

Wenn Sie das MathCityMap Portal durchforsten, werden Sie feststellen, dass Blumentöpfe für vielfältige geometrische Aufgabenstellungen dienen. Alleine durch das häufige Vorkommen und die verschiedenen Formen (Zylinder, Prisma mit sechseckiger Grundfläche, etc.) wird die Fragestellung, wie viel Liter Erde in einen Blumentopf passen, realisiert. In der heutigen Aufgabe der Woche handelt es sich um einen Blumentopf in Form eines Kegelstumpfs.

Aufgabe der Woche: Blumentopf (Aufgabennummer: 1219)

Wie viel Erde befindet sich in dem Blumentopf, wenn er bis oben gefüllt wird? Gib das Ergebnis in Litern an.

Das Volumen eines Kegelstumpfs ist wahrscheinlich nicht allen Schülern direkt geläufig. Entsprechend müssen verschiedene Strategien angewendet werden, beispielsweise die Differenz von einem großen und einem kleinen Kegel. Weitere Herausforderungen sind die Berechnung des unteren Radius‘ mithilfe des Umfangs sowie die Berücksichtigung des Randes/Bodens, der offensichtlich nicht mit Erde gefüllt ist.

Aufgabe der Woche: Kombinatorische Knobelaufgaben

Am Montag, den 14.05.2018 haben 45 mathematisch interessierte Grundschulkinder aus einem Enrichment-Programm der Uni Frankfurt mit MathCityMap den Campus Westend erkundet. Bei anfänglich gewittrigem Wetter sind die motivierten Dritt- und Viertklässler gemeinsam mit ihren Eltern und Studierenden auf mathematische Entdeckertour gegangen. Dabei wurden kombinatorische Knobeleien, wie die Baumaufgabe, und Messaufgaben kombiniert, sodass gemeinsam gerätselt und […]

Am Montag, den 14.05.2018 haben 45 mathematisch interessierte Grundschulkinder aus einem Enrichment-Programm der Uni Frankfurt mit MathCityMap den Campus Westend erkundet. Bei anfänglich gewittrigem Wetter sind die motivierten Dritt- und Viertklässler gemeinsam mit ihren Eltern und Studierenden auf mathematische Entdeckertour gegangen. Dabei wurden kombinatorische Knobeleien, wie die Baumaufgabe, und Messaufgaben kombiniert, sodass gemeinsam gerätselt und geknobelt wurde.

Aufgabe: Verbundene Bäume (Aufgabennummer: 3485)

Wie viele Seile müssten gespannt werden, wenn jeder Baum mit jedem verbunden sein soll?

Die Kinder hatten sichtlich Spaß dabei, gemeinsam eine Lösung für die Problemstellungen zu finden. Gerade bei der Baumaufgabe konnten sie an Vorwissen aus den Förderstunden anknüpfen, wo eine ähnliche Frage bei der Begrüßung mit Handschlag bereits thematisiert wurde. Die Erkenntnis, dass der erste der 15 Bäume mit 14 verbunden wird, der zweite mit 13 und so weiter führte schnell zum richtigen Ergebnis.

Auch die Fragen, auf wie viele Arten sich 6 Personen auf eine Bank setzen können, sowie die Anzahl der Möglichkeiten eine Treppe mit Einer-, Zweier- oder Dreierschritten hochzugehen konnten von den Kindern durch Rechnungen und Ausprobieren gelöst werden.

Besonderes Highlight war eine Aufgabe, deren richtige Lösung das Schloss einer Schatztruhe mit kleinen Überraschungen öffnete.

Aufgabe der Woche: Torbogen

Enstanden auf einer Lehrerfortbildung in Erfurt, betrachten wir heute die Aufgabe der Woche zum Thema Torbogen. Das Thema lässt verschiedene Fragestellungen zu, bereits vor einigen Wochen haben wir eine Torbogen-Aufgabe vorgestellt, in der es um das Gewicht der verwendeten Steine eines Torbogens ging. Heute steht die maximale Höhe des Torbogens im Fokus. Aufgabe: Torbogen (Aufgabennummer: […]

Enstanden auf einer Lehrerfortbildung in Erfurt, betrachten wir heute die Aufgabe der Woche zum Thema Torbogen. Das Thema lässt verschiedene Fragestellungen zu, bereits vor einigen Wochen haben wir eine Torbogen-Aufgabe vorgestellt, in der es um das Gewicht der verwendeten Steine eines Torbogens ging. Heute steht die maximale Höhe des Torbogens im Fokus.

Aufgabe: Torbogen (Aufgabennummer: 3090)

Bestimme die maximale Höhe des Torbogens an der Krämerbrücke. Gib das Ergebnis in Metern an. Gib dein Ergebnis gerundet auf zwei Nachkommastellen an.

Die wohl eleganteste Art die Aufgabe zu lösen ist die Unterteilung des Torbogens in Rechteck und Halbkreis:

Mit diesem Hinweis gilt es den Punkt zu bestimmen, an dem der Halbkreis beginnt und das Rechteck endet. Mit der Höhe des Rechtecks und dem Radius des Halbkreises (am besten zu ermitteln mithilfe des Durchmessers) ergibt sich die Höhe des Torbogens. Soll das Thema Kreis noch mehr in den Fokus gestellt werden, so könnte auch nach dem Umfang des Torbogens gefragt werden, sodass der Zusammenhang von Durchmesser und Umfang thematisiert werden könnte.