Strahlensatz | MathCityMap

Trail des Monats: Mathe auf dem Schulhof

Adrian Schrock, Mathelehrer an der Weibelfeldschule in Dreieich nahe Frankfurt, hat unseren neuen Trail des Monats erstellt. Die Aufgaben des Mathtrails drehen sich um die Themenfelder Pythagoras und Strahlensatz. Anhang dieses Beispiels wollen wir aufzeigen, wie Sie sogenannte themenbasierte Mathtrails mit enger curricularer Bindung erstellen können. Im Interview bereitet Adrian Schrock über seine Erfahrungen mit […]

Adrian Schrock, Mathelehrer an der Weibelfeldschule in Dreieich nahe Frankfurt, hat unseren neuen Trail des Monats erstellt. Die Aufgaben des Mathtrails drehen sich um die Themenfelder Pythagoras und Strahlensatz. Anhang dieses Beispiels wollen wir aufzeigen, wie Sie sogenannte themenbasierte Mathtrails mit enger curricularer Bindung erstellen können. Im Interview bereitet Adrian Schrock über seine Erfahrungen mit MathCityMap.

Wie nutzen Sie MCM und warum? Was ist das Besondere an Ihrem Trail?

Ich nutze den Trail „Unseren Schulhof mit Mathe entdecken“ aktuell in meiner 9. Klasse im Themenfeld „Satz des Pythagoras“ und „Strahlensätze“ und möchte damit die Motivation zum Problemlösen in der Klasse steigern.

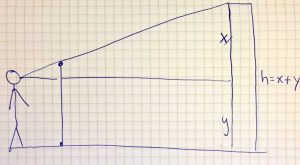
Besonders an meinem Trail ist, dass sich alle Aufgaben auf dem Schulhof befinden und die Themen „Satz des Pythagoras“ und „Strahlensätze“ verbinden. Es können nicht nur unzugängliche Größen wie die Höhe des Schulgebäudes berechnet werden, sondern auch durch die Umkehrung der Sätze sowohl der 90° Winkel als auch die Parallelität anhand von Objekten auf dem Schulhof überprüft werden.

Die erste Aufgabe ist explizit zum Einstieg in das Arbeiten mit dem Mathtrail gedacht und soll in Kleingruppen im Klassenraum durchgeführt werden. Dies habe ich bereits erfolgreich im Unterricht erprobt und hatte den Vorteil, dass die SuS die App zunächst kennenlernen und mögliche Fragen direkt im Plenum geklärt werden können. Zudem kann auf mögliche Schwierigkeiten bei der Verwendung des Geodreiecks als „Försterdreieck“ oder Messunggenauigkeiten eingegangen werden.

Um die Relevanz der Aufgabenstellungen zu erhöhen ist in meinen Beschreibungen „Über das Objekt“ eine kurze Geschichte formuliert, die darstellt warum die Fragestellung interessant sein könnte. Zum Beispiel: „Zwischen den Säulen kann jeweils eine Leinwand für ein Bühnenbild aufgehangen werden. Eine Lehrkraft will für eine Aufführung vom Darstellenden Spiel im Freilichttheater wissen, ob die Leinwände parallel zueinander stehen.“ Die Geschichten sind natürlich erdacht, beantworten allerdings eventuell die Frage der SuS „Wozu sollte man das wissen wollen?“.

Welche didaktischen Ziele verfolgen Sie?

Einerseits möchte mit dem Trail gezielt die Motivation zum Problemlösen in der 9. Klasse fördern. Durch Fokussierung auf die gewählten Themen hat der Trail andererseits den zusätzlichen Zweck die Unterrichtsinhalte an realen Objekten anwenden zu können und damit zu vertiefen. Der Vorteil daran ist, dass bei der Ausgangssituation der absolvierenden SuS klar ist, welches Vorwissen für den Trail erforderlich ist. Ein Nachteil ist natürlich, dass bei einer Bearbeitung von anderen Klassenstufen die Motivation eventuell geringer ist, da sie keinen Zusammenhang zu ihrem aktuellen Unterricht sehen.

Weitere Anmerkungen zu MCM?

Kleiner Wunsch an das MCM-Team: Beim Aufgaben-Wizard fehlen Aufgabentypen zur Bestimmung von Höhen oder Überprüfung beispielsweise der Parallelität oder ähnliches wie in meinem Trail. Eventuell könnte man hier noch ein paar Themenfelder ergänzen.

Den Aufbau der Website und vor allem die Rückmeldung zu den erstellten Aufgaben empfinde ich als sehr gut – ein Lob an die Mitarbeiter!

Aufgabe der Woche: Höhe der Skulptur

Zu Beginn des Monats hat Iwan Gurjanow das MathCityMap Projekt erfolgreich in Schweden auf der PME Konferenz vorgestellt. Natürlich wurden vor Ort auch Aufgaben angelegt, so wie die heutige Aufgabe der Woche. Aufgabe: Höhe der Statue (Aufgabennummer: 4303) Wie hoch ist die Statue? Gib das Ergebnis in Metern an. Die Aufgabe lässt sich auf verschiedene […]

Zu Beginn des Monats hat Iwan Gurjanow das MathCityMap Projekt erfolgreich in Schweden auf der PME Konferenz vorgestellt. Natürlich wurden vor Ort auch Aufgaben angelegt, so wie die heutige Aufgabe der Woche.

Aufgabe: Höhe der Statue (Aufgabennummer: 4303)

Wie hoch ist die Statue? Gib das Ergebnis in Metern an.

Die Aufgabe lässt sich auf verschiedene Arten lösen. Zum einen ist es aus einer größeren Entfernung möglich, mithilfe einer Person als Referenzgröße zu schätzen, wie oft diese Person in die Statue passt.

Genauer wird es, wenn die Aufgabe mithilfe des Strahlensatzes gelöst wird, wie im folgenden Hinweisbild dargestellt:

Als Referenz kann hier der Zollstock dienen.

Blaupausenaufgaben: Gebäudehöhe

Heute möchten wir Ihnen unsere Blaupausenaufgaben zum Thema Höhe von Gebäuden vorstellen. Dieses Thema bietet für verschiedene Klassenstufen die Möglichkeit, Mathematik zu machen. Die Höhe von Gebäuden kann bereits mit Schülerinnen und Schülern der Klassenstufe 5 bestimmt werden, wenn sich Regelmäßigkeiten und Muster erkennen lassen: https://mathcitymap.eu/en/portal-en/?show=task&id=2232 Diese können z.B. Backsteine, Glasscheiben oder Platten sein, wovon […]

Heute möchten wir Ihnen unsere Blaupausenaufgaben zum Thema Höhe von Gebäuden vorstellen. Dieses Thema bietet für verschiedene Klassenstufen die Möglichkeit, Mathematik zu machen.

Die Höhe von Gebäuden kann bereits mit Schülerinnen und Schülern der Klassenstufe 5 bestimmt werden, wenn sich Regelmäßigkeiten und Muster erkennen lassen: https://mathcitymap.eu/en/portal-en/?show=task&id=2232

Diese können z.B. Backsteine, Glasscheiben oder Platten sein, wovon man eine oder mehrere messen kann und dann durch die Gesamtanzahl auf die Gesamthöhe schließen kann. Eine solche Fragestellung schult also auch den mathematischen Blick für Regelmäßigkeiten und Muster in der Umwelt.

Die Schwierigkeit der Aufgabe steigt, sobald das Gebäude keine solcher Regelmäßigkeiten aufweist. Die Höhe lässt sich dann mithilfe des Strahlensatzes bestimmen.

https://mathcitymap.eu/en/portal-en/?show=task&id=1474

Dafür gibt es verschiedene Lösungsmöglichkeiten, beispielsweise mithilfe des Sonnenstandes bei geeigneter Wetterlage, mithilfe von kleineren Objekten (z.B. Laternen) oder mithilfe des Zollstocks. Hierbei ist es besonders hilfreich, sich vorab eine Skizze der Situation zu machen, um eine Anwendung des Strahlensatzes zu erleichtern.

Wichtig in beiden Fällen ist eine Kennzeichnung in Aufgabenstellung oder –bild, die deutlich macht, bis zu welcher Stelle die Höhe bestimmt werden soll, beispielsweise, wenn von Dachvorständen abgesehen werden soll.

Im beigefügten Dokument Höhe von Gebäuden finden Sie unsere ausführliche Darstellung beider Aufgabentypen.

Aufgabe der Woche: Ginnheimer Spargel

Die akutelle Aufgabe der Woche befasst sich mit einem der vielen Frankfurt Wahrzeichen: dem Europaturm, auch bekannt als „Ginnheimer Spargel“. In der dazugehörigen Aufgabe geht es darum, die eigene Entfernung zum Turm mithilfe des Strahlensatzes zu schätzen. Aufgabe: Ginnheimer Spargel (Aufgabennummer: 1595) Schätze die Entfernung von deinem Standort zum Ginnheimer Spargel (Telekom Sendeturm, Europaturm). Gib […]

Die akutelle Aufgabe der Woche befasst sich mit einem der vielen Frankfurt Wahrzeichen: dem Europaturm, auch bekannt als „Ginnheimer Spargel“. In der dazugehörigen Aufgabe geht es darum, die eigene Entfernung zum Turm mithilfe des Strahlensatzes zu schätzen.

Aufgabe: Ginnheimer Spargel (Aufgabennummer: 1595)

Schätze die Entfernung von deinem Standort zum Ginnheimer Spargel (Telekom Sendeturm, Europaturm). Gib das Ergebnis in Metern an. Zur Info: die Kanzel hat einen Durchmesser von 59 m.

Die erste Herausforderung besteht zunächst darin, einen geeigenten Lösungsweg zu finden. Mithilfe des Strahlensatzes lässt sich die Aufgabe mit Einsatz des eigenen Körpers lösen. Dafür werden Arm und Daumen so ausgestreckt, dass die Kanzel des Turms mit einem geöffneten Auge verdeckt ist. Anschließend lässt sich die Entfernung zum Ginnheimer Spargel über die Daumenbreite und die Armlänge bzw. Entfernung von Daumen zu Auge berechnen.

Die Aufgabe ist ein gelungenes Beispiel für „Outdoor mathematics“ indem die theoretischen Formeln (hier zu den Strahlensätzen) eine authentische Anwendung in der Umwelt finden. Zur Lösung der Aufgabe benötigen die SchülerInnen Wissen zu den Strahlensatz. Die Aufgabe lässt sich damit der Geometrie zuordnen und kann ab Klasse 9 gelöst werden.

Aufgabe der Woche: Beleuchtung des Schlossgartens

Diese Woche dreht sich die „Aufgabe der Woche“ um eine typische Anwendung der Strahlensätze. Insbesondere geht es dabei um die Höhenbestimmung von Objekten mithilfe der Strahlensätze. Dieser Aufgabentyp lässt sich auf viele verschiedene Objekte übertragen und findet sich dementsprechend in einigen MathCityMap Trails. Im hier beschriebenen Beispiel geht es um die Höhenbestimmung der Laternen im […]

Diese Woche dreht sich die „Aufgabe der Woche“ um eine typische Anwendung der Strahlensätze. Insbesondere geht es dabei um die Höhenbestimmung von Objekten mithilfe der Strahlensätze. Dieser Aufgabentyp lässt sich auf viele verschiedene Objekte übertragen und findet sich dementsprechend in einigen MathCityMap Trails. Im hier beschriebenen Beispiel geht es um die Höhenbestimmung der Laternen im Erlangener Schlossgarten aus dem Trail „Rund um den Erlangener Schlossgarten“.

Aufgabe: Beleuchtung des Schlossgartens (Aufgabennummer: 709)

Bestimme näherungsweise die Höhe der im Schlossgarten aufgestellten zweiflammigen Bogenlampen in der Einheit cm.

Um die Aufgabe zu lösen, wird der zweite Strahlensatz benötigt. Dafür positionieren sich die SchülerInnen wenige Meter vom Objekt entfernt und fixieren das Objekt. Anschließend kann mithilfe des Zollstocks der Strahlensatz zur Anwendung gebracht werden. Dafür sind die Augenhöhe sowie der Abstand zum Objekt zu messen. Mit ausgestrecktem Arm wird der Zollstock so gehalten, dass sich die Zollstockspitze mit dem oberen Ende der Laterne deckt. Die Länge des ausgestreckten Arms und die Maßstabslänge, die der Laternenhöhe ab Augenhöhe entspricht, führen zur Höhe der Laterne.

Es handelt sich hierbei um eine Problemlösesituation, in der zunächst fehlende Größen durch eine geeignete Ausgangssituation ermittelt werden müssen. Die Anwendung des Strahlensatzes kann dabei insbesondere durch die Anfertigung einer Skizze erleichtert werden. Die Aufgabe eignet sich insbesondere um den SchülerInnen die praktische Anwendung des Strahlensatzes aufzuzeigen und dem Kalkül eine inhaltliche Bedeutung zu verleihen.