Höhe | MathCityMap

Aufgabe der Woche: Höhe der Skulptur

Zu Beginn des Monats hat Iwan Gurjanow das MathCityMap Projekt erfolgreich in Schweden auf der PME Konferenz vorgestellt. Natürlich wurden vor Ort auch Aufgaben angelegt, so wie die heutige Aufgabe der Woche. Aufgabe: Höhe der Statue (Aufgabennummer: 4303) Wie hoch ist die Statue? Gib das Ergebnis in Metern an. Die Aufgabe lässt sich auf verschiedene […]

Zu Beginn des Monats hat Iwan Gurjanow das MathCityMap Projekt erfolgreich in Schweden auf der PME Konferenz vorgestellt. Natürlich wurden vor Ort auch Aufgaben angelegt, so wie die heutige Aufgabe der Woche.

Aufgabe: Höhe der Statue (Aufgabennummer: 4303)

Wie hoch ist die Statue? Gib das Ergebnis in Metern an.

Die Aufgabe lässt sich auf verschiedene Arten lösen. Zum einen ist es aus einer größeren Entfernung möglich, mithilfe einer Person als Referenzgröße zu schätzen, wie oft diese Person in die Statue passt.

Genauer wird es, wenn die Aufgabe mithilfe des Strahlensatzes gelöst wird, wie im folgenden Hinweisbild dargestellt:

Als Referenz kann hier der Zollstock dienen.

Blaupausenaufgaben: Gebäudehöhe

Heute möchten wir Ihnen unsere Blaupausenaufgaben zum Thema Höhe von Gebäuden vorstellen. Dieses Thema bietet für verschiedene Klassenstufen die Möglichkeit, Mathematik zu machen. Die Höhe von Gebäuden kann bereits mit Schülerinnen und Schülern der Klassenstufe 5 bestimmt werden, wenn sich Regelmäßigkeiten und Muster erkennen lassen: https://mathcitymap.eu/en/portal-en/?show=task&id=2232 Diese können z.B. Backsteine, Glasscheiben oder Platten sein, wovon […]

Heute möchten wir Ihnen unsere Blaupausenaufgaben zum Thema Höhe von Gebäuden vorstellen. Dieses Thema bietet für verschiedene Klassenstufen die Möglichkeit, Mathematik zu machen.

Die Höhe von Gebäuden kann bereits mit Schülerinnen und Schülern der Klassenstufe 5 bestimmt werden, wenn sich Regelmäßigkeiten und Muster erkennen lassen: https://mathcitymap.eu/en/portal-en/?show=task&id=2232

Diese können z.B. Backsteine, Glasscheiben oder Platten sein, wovon man eine oder mehrere messen kann und dann durch die Gesamtanzahl auf die Gesamthöhe schließen kann. Eine solche Fragestellung schult also auch den mathematischen Blick für Regelmäßigkeiten und Muster in der Umwelt.

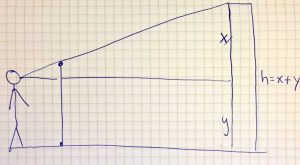
Die Schwierigkeit der Aufgabe steigt, sobald das Gebäude keine solcher Regelmäßigkeiten aufweist. Die Höhe lässt sich dann mithilfe des Strahlensatzes bestimmen.

https://mathcitymap.eu/en/portal-en/?show=task&id=1474

Dafür gibt es verschiedene Lösungsmöglichkeiten, beispielsweise mithilfe des Sonnenstandes bei geeigneter Wetterlage, mithilfe von kleineren Objekten (z.B. Laternen) oder mithilfe des Zollstocks. Hierbei ist es besonders hilfreich, sich vorab eine Skizze der Situation zu machen, um eine Anwendung des Strahlensatzes zu erleichtern.

Wichtig in beiden Fällen ist eine Kennzeichnung in Aufgabenstellung oder –bild, die deutlich macht, bis zu welcher Stelle die Höhe bestimmt werden soll, beispielsweise, wenn von Dachvorständen abgesehen werden soll.

Im beigefügten Dokument Höhe von Gebäuden finden Sie unsere ausführliche Darstellung beider Aufgabentypen.

Aufgabe der Woche: Gebäudehöhe

Durch Kooperation mit der MOOC Arbeitsgruppe der Universität Turin, freuen wir uns über erste MCM Aufgaben in Italien, wo auch die heutige Aufgabe der Woche angelegt ist. Aufgabe: Gebäudehöhe (Aufgabennumer: 2045) Bestimme die Höhe des Gebäudes. Gib das Ergebnis in Metern an. Die Höhe lässt sich auf verschiedene Weisen annähern, z.B. durch Schätzen oder den […]

Durch Kooperation mit der MOOC Arbeitsgruppe der Universität Turin, freuen wir uns über erste MCM Aufgaben in Italien, wo auch die heutige Aufgabe der Woche angelegt ist.

Aufgabe: Gebäudehöhe (Aufgabennumer: 2045)

Bestimme die Höhe des Gebäudes. Gib das Ergebnis in Metern an.

Die Höhe lässt sich auf verschiedene Weisen annähern, z.B. durch Schätzen oder den Strahlensatz. Besonders elegant kann man die Aufgabe lösen, indem man nach Strukturen und Mustern in der Gebäudefassade sucht. Bei diesem Gebäude fallen direkt die Querstreifen auf, die sich bis zum Dach finden lassen. Für die Gesamthöhe ist es also nur nötig, die Höhe eines Querstreifens zu ermitteln, sowie die Anzahl der Streifen zu zählen. Kleinere Abweichungen vom Muster können mithilfe von Schätzungen angenähert werden.

Mithilfe dieser Methode kann die Aufgabe bereits von SchülerInnen der Klassenstufe 6 gelöst werden. Bei älteren SchülerInnen werden die verschiedenen Lösungsmöglichkeiten im besten Fall vor Ort diskutiert und anhand der Einfachheit und Genauigkeit bewertet.